Скорость. Пусть точка, двигаясь по криволинейной траектории, про­шла за малый промежуток времени At малый путь AS (рис

Пусть точка, двигаясь по криволинейной траектории, про­шла за малый промежуток времени At малый путь AS (рис. 2).

Проведем касательную АС к траектории в точке А и хорду АВ. Тогда отношение пути, пройденного материальной точкой, к промежутку времени, за который этот путь пройден, называ­ется средней скалярной скоростью движения

v_ср=

(1)

Измеряется в метрах в секунду (м/с). Средней скоростью пере­мещения У™ за промежуток времени Д1 называется вектор, рав-вый отношению вектора перемещения AS за промежуток време­ни At к величине этого промежутка времени:

v_ср= (2)

Для полноты характеристики движения вводится понятие мгно­венной скорости (скорости в данный момент времени в данной точке пути).

Мгновенная скорость – это вектор, направленный по касательной к траектории, а по величине равный пределу отношения перемещения 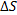к промежутку времени 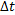, за который этот путь пройден,при стремлении промежутка времени к нулю

V= 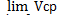= = 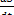(3)

Если скорость не изменяется с течением времени, то движение материальной точки называется равномерным (t> = const), в про­тивном случае — движение называется неравномерным.

Ускорение

Неравномерность движения (в Ф const) характеризуется фи­зической величиной — ускорением.

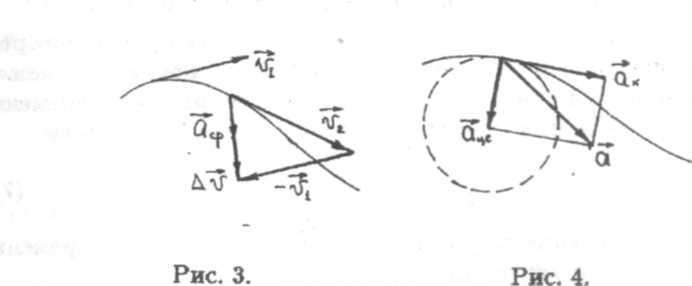
Пусть материальная точка за малый промежуток времени At из точки А, где она имела скорость v_b переместилась в точ­ку В, где она имела скорость v₂ (рис. 3). Изменение скорости есть вектор Av, равный разности векторов конечной и началь­ной скоростей, т.е. v = v₂ — v₁.

Отношение изменения вектора скорости к тому промежут­ку времени, за который это изменение произошло, называется средним ускорением.

a_ср= 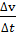(4)

В общем случае среднее ускорение может быть различным на различных участках траектории и при t 0 оно превращается в мгновенное ускорение. Для наглядности ограничимся случа­ем плоской кривой. Тогда мгновенное ускорение — это вектор направленный под углом к траектории в сторону ее вогнутости, а по модулю равный пределу отношения изменения скорости Av к промежутку времени At при стремлении At к нулю (рис. 3)

a= 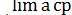= = 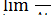= 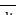v (5)

Согласно формулам (4) и (5), ускорение измеряется в (м/с2).

Полное ускорение апринято раскладывать на две составля­ющие (рис. 4), одна из которых направлена по касательной к траектории и называется касательным или тангенциальным ускорением (аг), другая - по нормали и называется нормаль­ным или центростремительным ускорением (а„).Очевидно, что

а = аг + аn; а = 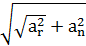(6)

Касательное ускорение изменяет только значение скорости, а центростремительное — только ее направление.

Если ускорение является величиной постоянной (а — const), то движение называется равнопеременным (при а > 0 — рав­ноускоренное движение, при о < 0 — равнозамедленное движе­ние). Таким образом, при поступательном движении твердого тела все его точки описывают совершенно одинаковые линии и имеют одинаковую скорость и одинаковое ускорение (в данный момент времени).