Равнопеременное прямолинейное движение
В этом случае аn= О, аt = а= const и мгновенное ускорение равно среднему ускорению за любой промежуток времени. Получим выражение скорости и пути в зависимости от времени для этого движения. Учитывая, что а = (v — vo)/t, получим:
v=v0 + at (7)
где v0 — начальная скорость, а v — скорость в момент времени t. Так как v = ds/dt, то dS = v • dt; тогда
S = 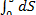 =
= 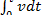 =
= 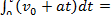
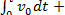
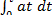 = v0t +
= v0t + 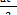 ;
;
S = v0t + 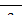 . (8)
. (8)
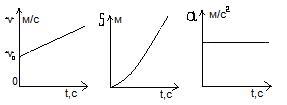
Рис. 5.
Подставляя выражение для t (t =(v-v0)/a) полученное из
уравнения (6), в (7), получим:
s = v0 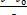 +
+ 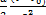 =
=  (2v0 + v - v0 ) =
(2v0 + v - v0 ) = 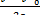 ,
,
откуда
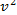 -
- 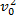 = 2aS
= 2aS
Если начальная скорость v0 = 0, то получим следующие выражения:
v=at; S = 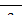 ;
; 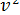 = 2aS.
= 2aS.
Согласно формулам (7) и (8), графики зависимостей v(t), S(t) и а(t) выглядят, как показано на рис. 5.
Для свободно падающего тела в безвоздушном пространстве а = g - 9.8 м/с2; тогда уравнения будут иметь вид
v = v0 + gt; h = v0t+ 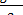 ; v2 -
; v2 - 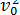 = 2gh.
= 2gh.
Если v — const, то движение называется равномерным. В этом случае a = 0, и согласно формуле (7)
S = vt. (11)
Графики пути и скорости изображены на рис. 6.
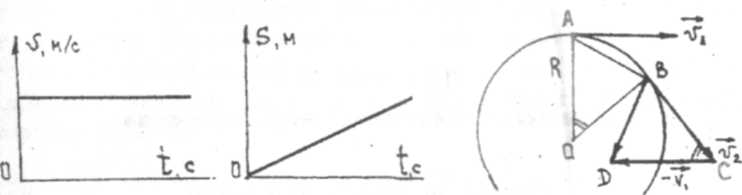
| Рис. 6. Рис. 7. |
Равномерное движение материальной точки по окружности
Движение материальной точки по окружности происходит с постоянной по модулю скоростью — аr = 0, а = аn. Определим центростремительное ускорение (рис. 7).
Углы АОВ и BCD равны как углы со взаимно перпендикулярными сторонами, v1 = v2 = v = const. Следовательно,  АОВ и
АОВ и  BCD подобны как равнобедренные с одинаковыми углами при вершине. Поэтому
BCD подобны как равнобедренные с одинаковыми углами при вершине. Поэтому
 =
= 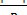 и
и 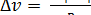 .
.
Тогда согласно формуле (4), запишем
 = a =
= a = 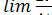 =
= 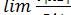 =
= 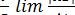 .
.
При  t, стремящемся к нулю, хорда АВ стремится к дуге
t, стремящемся к нулю, хорда АВ стремится к дуге  S; поэтому
S; поэтому
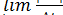 =
= 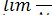 = v;
= v; 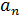 =
= 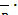 =
=  . (12)
. (12)
Рисунок 7 позволяет еще раз убедиться, что полученное ускорение действительно является центростремительным, т.к. при 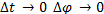 При этом вектора
При этом вектора  v и а, имеющие одинаковое направление, будут направлены вдоль радиуса окружности к ее центру О. Наряду с линейной скоростью (v) равномерное движение материальной точки по окружности можно характеризовать угловой скоростью
v и а, имеющие одинаковое направление, будут направлены вдоль радиуса окружности к ее центру О. Наряду с линейной скоростью (v) равномерное движение материальной точки по окружности можно характеризовать угловой скоростью 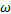 , но об этом поговорим в лекции №5.
, но об этом поговорим в лекции №5.
Лекция N«2
Дата добавления: 2015-08-11; просмотров: 643;
