Селективне рефокусування за допомогою ІГП когерентностей різного порядку

За відсутності градієнта поля Ларморова частота, w, спіну визначається прикладеним магнітним полем В₀. При цьому w=gВ₀. Якщо додатково прикласти імпульсний градієнт вздовж осі z, з'являється додаткове поле В_g(z), що пов'язане із градієнтом. За таких умов Ларморова частота спінів, в залежності від їхнього розташування вздовж осі z буде визначатися сумою обох цих полів:

w_(z) = g (B₀ + B_g(z)) рад с^-1 (5.1)

Якщо тривалість імпульсу градієнта становить t_g сек., вектор намагніченості під його дією повертається на фазовий кут Ф:

Ф_(z) = g (B₀ + B_g(z)) t_g = gB₀t_g + gB_g(z)t_g (5.2)

Перший член останнього співвідношення описує Ларморову прецесію без градієнта. Вона постійна у всьому об’ємі зразка. Тому ми виключаємо його з подальшого обговорення. Другий член описує специфічну залежність фази, викликану дією градієнта. Нас буде цікавити саме ця залежність.

Наведене вище рівняння можна використовувати лише для одноквантової когерентності. Йогу узагальнення можна досягти, якщо включити в нього член, що описує порядок когерентності р (тобто сумарну зміну спіну переходу). У результаті одержимо:

Ф_(z) = pgB_g(z)t_g (5.3)

З даної модифікації рівняння витікає висновок, що р-квантова когерентність розфазується зі швидкістю, що пропорційна р. Так, двохквантова когерентність розфазується вдвічі швидше одноквантової когерентності. Аналогічно, нуль-квантова когерентність нечутлива до дії імпульсних градієнтів. Якщо когерентність включає ядра різних типів, слід враховувати також і гіромагнітне співвідношення для кожного ядра:

Ф_(z) = B_g(z) t_g∑ p_i g_i (5.4)

Таким чином, ми доходимо висновку про те, що ступінь рефокусування залежить від порядку когерентності і гіромагнітного співвідношення ядра. Це дає ключ до селекції сигналів методом імпульсних градієнтів. Метою застосування градієнтів у більшості експериментів є вибіркове рефокусування намагніченості, що пов'язана з обраним шляхом перенесення когерентності. Інші шляхи видаляються через їх розфокусування і тому не проявляються в кінцевому спектрі. Хоча самі ІГП не можуть змінити порядок когерентності, це можна зробити за допомогою радіочастотних імпульсів. Комбінація радіочастотних імпульсів, що продукують когерентність потрібного порядку, і імпульсних градієнтів для її виділення дозволяє в кінцевому спектрі одержати необхідний результат.

Приклад такої селекції для гомоядерної спінової системи, зображений на Рис. 5.33.

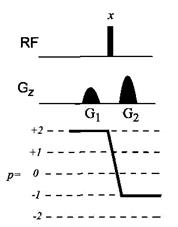
Рис.5.33. Ілюстрація селекції сигналу за допомогою імпульсного градієнта поля. Використання двох градієнтів з відношенням G₁:G₂ = 1:2 виділяє тільки показаний шлях перенесення когерентності, залишаючи всі інші розфокусованими і невидимими.

Нехай на початку експерименту присутня тільки двохквантова когерентність. Таким чином, до подачі радіочастотного імпульсу є когерентність із р = 2. Нашою метою є переведення її в когерентність порядку р=-1. Розрахуємо, які градієнтні імпульси слід використати для досягнення цієї мети. Будемо вважати, що спочатку на двохквантову когерентність впливає градієнт із полем В_g1 тривалістю t_1. Цей градієнт викличе певний фазовий зсув сигналів. Його можна обчислити за формулою:

Ф₁ = 2gB_g1t₁ (5.5)

Наступний радіочастотний імпульс перерозподілить когерентність між всіма можливими станами і частину її перетворить у цільову одноквантову намагніченість порядку р = -1. Далі подається градієнтний імпульс потужністю B_g2 й тривалістю t₂, що фазує когерентність:

Ф₂ = -gB_g2t₂ (5.6)

Для когерентності з обраним шляхом переходу, рефокусування відбувається в тому випадку, коли сумарна залежність фази від градієнтних імпульсів дорівнює нулю.

∑Ф_i = ∑gB_git_i = 0 (5.7)

іншими словами, рефокусування під впливом останнього градієнтного імпульсу повинно нейтралізувати розфокусування під впливом всіх попередніх градієнтних імпульсів. Так, у наведеному вище прикладі Ф₂ повинно бути еквівалентним Ф₁. Цього можна досягти або зміною тривалості другого градієнтного імпульсу відносно першого, при сталості його амплітуди, або зміною амплітуди при незмінній тривалості. Зараз прийнято використовувати градієнтні імпульси однакової тривалості і змінної амплітуди. Тому в нашому прикладі В_g2 = 2В_g1. Таким чином, амплітуда другого градієнтного імпульсу повинна бути вдвічі більшою, ніж у першого. У цьому випадку виділяється необхідний шлях когерентності (рис. 5.33).

На відміну від одноквантової намагніченості, трьохквантова когерентність, що теж може виникнути в нашому експерименті, для якої р = 3, вимагає для рефокусування сумарної фази

Ф = (3gB_g1t_g1) + (-1g2B_g1t₁) = gB_g1t₁ (5.8)

Тому вона залишається розфазованою і не дає внеску в спостережуваний сигнал. Таким чином, градієнтні імпульси виділяють тільки необхідний шлях зміни когерентності. Для гомоядерних систем при використанні градієнтів однакової тривалості необхідно знати тільки порядки когерентності і у згоді з ними задавати відношення амплітуд градієнтів. Для гетероядерних систем при розрахунку інтенсивностей градієнтних імпульсів слід враховувати також гіромагнітні співвідношення ядер. Оскільки у всіх наступних обговореннях градієнти мають однакову форму та тривалість, ми будемо позначати їх G_i, маючи на увазі, що вони мають інтенсивність В_gi і тривалість t_i.