Інтерпретація структури мультиплетів

Важлива частина аналізу одномірних спектрів полягає у вимірюванні КССВ окремих мультиплетів. Це дозволяє отримати зі спектра максимальну структурну інформацію. Хоча це завдання є досить простим для добре розділених мультиплетів, воно багаторазово ускладнюється для сигналів, що перекриваються. У таких випадках можна скористатися перевагами двомірних спектрів, у яких кроспіки сигналів, що перекриваються, можуть спостерігатися окремо. У цьому розділі буде показано, як визначити величини КССВ, виходячи з мультиплетної структури кроспіків.

Перш за все, треба завжди мати на увазі, що кроспіки у двомірному спектрі виникають за рахунок перенесення когерентності від протифазних компонентів мультиплетів на спіново-зв’язані з ними сигнали. Як було показано раніше, спінова взаємодія в кроспіку проявляється як протифазне розщеплення у двох вимірах, тому для двохспінової системи в результаті отримуємо протифазний квадрат (Рис. 5.36).

Рис. 5.36. Квадрат протифазних розщеплень для активних J_ax, між двома спінами A і X, що мають кореляцію. Такий вид мають мультиплети всіх кроспіків в експерименті COSY.

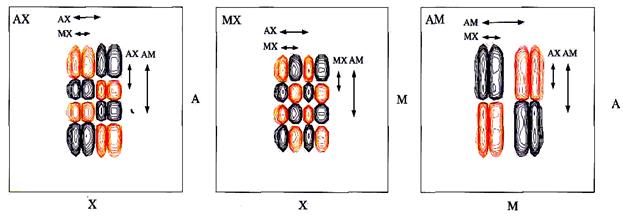
КССВ, J_AX, показана на Рис. 5.36, називається активною, оскільки саме завдяки ній відбувається утворення кроспіку. У двохспіновій системі існує лише активна КССВ. Якщо ж маємо більш складну спінову систему, то окрім неї сигнал може мати і інші розщеплення. Ці розщеплення зумовлені пасивними КССВ. Вони, хоча і впливають на мультиплетність кроспіка, не зумовлюють його появу завдяки явищу переносу когерентності. Тому такі КССВ не мають протифазної орієнтації компонентів мультиплету. Кожна КССВ є активною відносно того кроспіка, появу якого вона зумовлює і пасивною відносно інших кроспіків, де вона також проявляється. Пасивні КССВ мають співфазне розщеплення і проявляються в протифазному масиві активних розщеплень як компоненти з незмінним знаком фази. Ці особливості та основні принципи аналізу мультиплетної структури можна проілюструвати на прикладі кроспіка трьохспінової системи АМХ, у якій J_AM>J_AX>J_MX (Рис. 5.37). Будемо вважати, що в кроспіку МХ, який містить протифазний квадрат, що відповідає активній КССВ J_MX, розташовується у верхньому лівому куті. Цей фрагмент репродукується з незмінною фазою великою пасивною КССВ J_АХ у напрямку f₂ і константою J_АМ відносно f₁.

Рис. 5.37.Структура кроспіків у фазочутливому COSY спектрі трьохспінової системи AMX. Стрілки вказують розщеплення для позначених КССВ. Спектр був розрахований для J_am = 18, J_Ax = 12 і J_Mx = 6 Гц. Цифрове розділення було 2,3 Гц/точка в кожному вимірі.

У результаті одержуємо структуру мультиплету, що містить 4х4 компонентів. Такий покроковий аналіз розщеплення є повністю аналогічним до того, що використовується в одномірній спектроскопії при побудові «дерев» мультиплетів. Структура мультиплету АХ у напрямку f₂ визначається великим протифазним розщепленням відповідно до J_АХ і подальшим розщепленням, зумовленим меншою пасивною J_МХ. У результаті структура піка в даному вимірі буде ++--. У вимірі f₁ активна КССВ є найменшою, тому знаки компонентів повторюються і одержуємо +-+-. Нарешті, мультиплет АМ містить дуже велику активну константу J_АМ в обох вимірах. При цьому утворюється протифазний квадрат, що охоплює весь мультиплет. Подальше розщеплення з меншими пасивними КССВ ядра Х приводить до подвоєння кожного з компонентів. Таким чином, правила інтерпретації структури двомірних мультиплетів аналогічні до тих, які застосовуються в одномірній спектроскопії з урахуванням існування активних і пасивних констант. Якщо взаємодія відбувається між одним спіном і n еквівалентними протонами, то мультиплетна структура може бути описаною, якщо вважати, що тільки з одним протоном є активна КССВ, а з іншими – пасивна. Тому для взаємодії з однаковими спінами можна побудувати протифазний аналог звичайного трикутника Паскаля (Рис. 5.38). Так для системи А₃Х кроспік містить дублет для А і +1+1-1-1 квартет для Х (Рис. 5.39).

Рис.5.38. (а) Трикутник Паскаля для 1D мультиплетів і (б) Протифазний еквівалент для передбачення структури мультиплетів COSY для розщеплення сигналів n еквівалентних спінів.

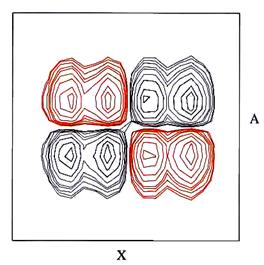
Рис. 5.39.COSY кроспік для групи A₃X ілюструє структуру, передбачену за допомогою трикутника Паскаля.

У реальних системах структура мультиплету може визначатися багатьма КССВ, причому всі вони можуть і не розділятися. Це приводить до перекривання компонентів мультиплетів і взаємного знищення деяких з них. Здебільшого при цьому спостерігається видиме спрощення структури мультиплетів. Часто в таких випадках малі КССВ не проявляються, як це показано для одного із кроспіків на рис. 5.37. Для детального аналізу тонкої структури, іноді корисним буває розглянути обидва еквівалентних кроспіки, що розташовані дзеркально відносно діагоналі. Вони можуть трохи розрізнятися через відмінність ступеня оцифровування у двох вимірах.

Вимірювання констант у такий спосіб обмежене шириною лінії компонентів мультиплетів, які у двомірних спектрах для малих молекул і молекул середнього розміру визначаються в основному цифровим розділенням, а не природною шириною лінії. За таких умов лінії, що перебувають у фазі, мають тенденцію до об'єднання з утворенням одного піка, що маскує КССВ. Протифазні компоненти залишаються розділеними, але відстань між ними може трохи перевищувати величину КССВ. Показано, що зменшення видимого розщеплення протифазних компонентів мультиплету дорівнює 0,6 ширини лінії (Рис. 5.40). Подальше зменшення розщеплення приводить до зменшення інтенсивності піків, або до повного їхнього зникнення. Звідси можна зробити висновок про неможливість вимірювання КССВ, що є істотно меншими від ширини лінії після оцифровування. Практично величина розщеплення повинна бути в 1,5 рази більшою від оцифрованої ширини лінії. Тому спектри повинні бути виміряні з достатнім цифровим розділенням по f₂.

Рис 5.40.Розділення протифазних піків як функція констант розщеплення і ширини лінії. Коли константи розщеплення стають відносно меншими, виміряні розщеплення (суцільна лінія) відхиляються від істинних значень (пунктирна лінія), що приводить до завищених значень констант.

Звідси також витікає, що кроспіки можуть зникати зі спектра COSY якщо ширина лінії є більшою або цифрове розділення є меншим від величини активної константи. Тому кроспіки, що викликані малими КССВ або широкими лініями можуть бути загубленими. Це є великою проблемою для дуже великих молекул, які мають велику природну ширину сигналів. У цьому випадку набагато кращі результати можна одержати із застосуванням TOCSY, оскільки компоненти мультиплетів кроспіків у цьому випадку завжди перебувають у фазі. Існують також більш прогресивні методи, які дозволяють вимірювати константи взаємодії в складних мультиплетах. Наприклад, метод DISCO дозволяє після одержання спектра COSY робити додавання і віднімання окремих інкрементів і в такий спосіб одержувати спрощені спектри, що містять тільки деякі сигнали. Тому вимірювання КССВ стають більш надійними.