При наличии перепада температур тела изменяют свои размеры, причем прямо пропорционально этому перепаду температур.
Пусть имеется перепад температур 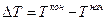 . Тогда этот закон имеет вид:
. Тогда этот закон имеет вид:
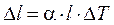
Здесь α - коэффициент линейного температурного расширения, l - длина стержня, Δ l-его удлинение.
4) Закон ползучести.
Исследования показали, что все материалы сильно неоднородны в малом. Схематическое строение стали изображено на рис.8.2.
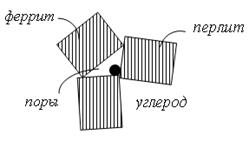
Рис.8.2.
Некоторые из составляющих обладают свойствами жидкости, поэтому многие материалы под нагрузкой с течением времени получает дополнительное удлинение 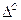 (рис.8.3.) (металлы при высоких температурах, бетон, дерево, пластики – при обычных температурах). Это явление называется ползучестьюматериала.
(рис.8.3.) (металлы при высоких температурах, бетон, дерево, пластики – при обычных температурах). Это явление называется ползучестьюматериала.

Рис.8.3.
Для жидкости справедлив закон: чем больше сила, тем больше скорость движения тела в жидкости. Если это соотношение линейно (т.е. сила пропорциональна скорости), то можно записать его в виде:
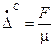
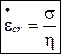 Если перейти к относительным силам и относительным удлинениям, то получим
Если перейти к относительным силам и относительным удлинениям, то получим
Здесь индекс « cr » означает, что рассматривается та часть удлинения, которая вызвана ползучестью материала. Механическая характеристика 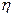 называется коэффициентом вязкости.
называется коэффициентом вязкости.
5) Закон сохранения энергии.
Рассмотрим нагруженный брус
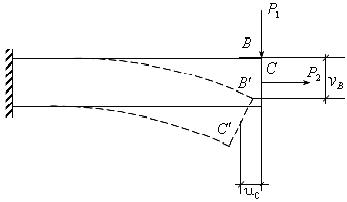
Рис.8.4.
Введем понятие перемещения точки, например,
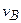 - вертикальное перемещение точки В;
- вертикальное перемещение точки В;
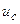 - горизонтальное смещение точки С.
- горизонтальное смещение точки С.
Силы 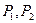 при этом совершают некоторую работу U. Учитывая, что силы
при этом совершают некоторую работу U. Учитывая, что силы 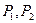 начинают возрастать постепенно и предполагая, что возрастают они пропорционально перемещениям, получим:
начинают возрастать постепенно и предполагая, что возрастают они пропорционально перемещениям, получим:
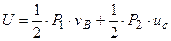 .
.
Согласно закону сохранения: никакая работа не исчезает, она тратится на совершение другой работы или переходит в другую энергию(энергия – это работа, которую может совершить тело.).
Работа сил 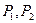 , тратится на преодоление сопротивления упругих сил, возникающих в нашем теле. Чтобы подсчитать эту работу учтем, что тело можно считать состоящим из малых упругих частиц. Рассмотрим одну из них:
, тратится на преодоление сопротивления упругих сил, возникающих в нашем теле. Чтобы подсчитать эту работу учтем, что тело можно считать состоящим из малых упругих частиц. Рассмотрим одну из них:

Рис.8.5.
Со стороны соседних частиц на него действует напряжение  . Равнодействующая напряжений будет
. Равнодействующая напряжений будет 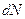
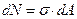
Под действием  частица удлинится. Согласно определению относительное удлинение это удлинение на единицу длины. Тогда:
частица удлинится. Согласно определению относительное удлинение это удлинение на единицу длины. Тогда:

Вычислим работу dW, которую совершает сила dN (здесь также учитывается, что силы dN начинают возрастать постепенно и возрастают они пропорциональны перемещениям):
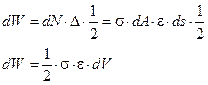
Для всего тела получим:
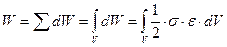 .
.
Работа W, которую совершило  , называют энергией упругой деформации.
, называют энергией упругой деформации.
Согласно закону сохранения энергии:
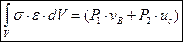
6)Принцип возможных перемещений.
Это один из вариантов записизакона сохранения энергии.
Пусть на брус действуют силы F1, F2, …. Они вызывают в теле перемещения точки 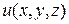 и напряжения
и напряжения  . Дадим телу дополнительные малые возможные перемещения
. Дадим телу дополнительные малые возможные перемещения 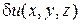 . В механике запись вида
. В механике запись вида 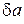 означает фразу «возможное значение величины а ». Эти возможные перемещения вызовут в теле дополнительные возможные деформации
означает фразу «возможное значение величины а ». Эти возможные перемещения вызовут в теле дополнительные возможные деформации 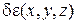 . Они приведут к появлению дополнительных внешних сил и напряжений
. Они приведут к появлению дополнительных внешних сил и напряжений 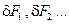 , δs.
, δs.
Вычислим работу внешних сил на дополнительных возможных малых перемещениях:
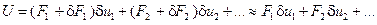
 |
Рис.8.6.
Здесь 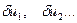 - дополнительные перемещения тех точек, в которых приложены силы F1, F2, …
- дополнительные перемещения тех точек, в которых приложены силы F1, F2, …
Рассмотрим снова малый элемент с поперечным сечением dA и длиной dz (см. рис.8.5. и 8.6.). Согласно определению дополнительное удлинение Ddz этого элемента вычисляется по формуле:
Ddz = de dz.
Сила растяжения элемента будет:
dN = (s+δs) dA ≈ s dA..
Работа внутренних сил на дополнительных перемещениях вычисляется для малого элемента следующим образом:
dW = dN Ddz = s dA de dz = sde dV
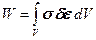 Суммируя энергию деформации всех малых элементов получим полную энергию деформации:
Суммируя энергию деформации всех малых элементов получим полную энергию деформации:
Закон сохранения энергии W = U дает:
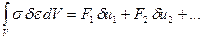 .
.
Это соотношение и называется принципом возможных перемещений (его называют также принципом виртуальных перемещений). Аналогично можно рассмотреть случай, когда действуют еще и касательные напряжения. Тогда можно получить, что к энергии деформации W добавится следующее слагаемое:
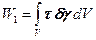
Здесь t - касательное напряжение, g -сдвиг малого элемента. Тогда принцип возможных перемещений примет вид:
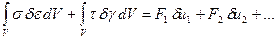
В отличие от предыдущей формы записи закона сохранения энергии здесь нет предположения о том, что силы начинают возрастать постепенно, и возрастают они пропорционально перемещениям
7) Эффект Пуассона.
Рассмотрим картину удлинения образца:
 |
Рис.8.7
Явление укорочения элемента тела поперек направления удлинения называется эффектом Пуассона.
Найдем продольную относительную деформацию.
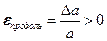
Поперечная относительная деформация будет:
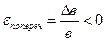
Коэффициентом Пуассона называется величина:
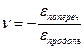
Для изотропных материалов (сталь, чугун, бетон) коэффициент Пуассона
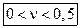
Это означает, что в поперечном направлении деформация меньше продольной.
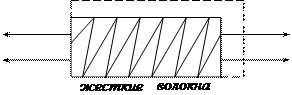
Примечание: современные технологии могут создать композиционные материалы, у которых коэффициент Пуассон >1, то есть поперечная деформация будет больше, чем продольная. Например, это имеет место для материала, армированного жесткими волокнами под малым углом 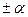 <<1 (см. рис.8.8.). Оказывается, что коэффициент Пуассона при этом почти пропорционален величине
<<1 (см. рис.8.8.). Оказывается, что коэффициент Пуассона при этом почти пропорционален величине 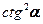 , т.е. чем меньше
, т.е. чем меньше 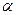 , тем больше коэффициент Пуассона.
, тем больше коэффициент Пуассона.
 | |||
 | |||
Рис.8.8. Рис.8.9
Еще более удивительным является материал, приведенный на (рис.8.9.), причем для такого армирования имеет место парадоксальный результат – продольное удлинение ведет к увеличению размеров тела и в поперечном направлении.
8) Обобщенный закон Гука.
 Рассмотрим элемент, который растягивается в продольном и поперечном направлениях. Найдем деформацию, возникающую в этих направлениях.
Рассмотрим элемент, который растягивается в продольном и поперечном направлениях. Найдем деформацию, возникающую в этих направлениях. 
Вычислим деформацию 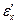 , возникающую от действия
, возникающую от действия 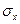 :
:
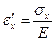
Рассмотрим деформацию от действия 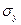 , которая возникает в результате эффекта Пуассона:
, которая возникает в результате эффекта Пуассона:
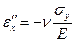
Общая деформация будет:

Если действует и 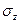 , то добавиться еще одно укорочение в направлении оси x
, то добавиться еще одно укорочение в направлении оси x 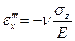 .
.
Следовательно: 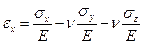
Аналогично: 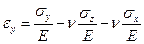
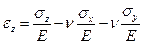
Эти соотношения называются обобщенным законом Гука.
Интересно, что при записи закона Гука делается предположение о независимости деформаций удлинения от деформаций сдвига (о независимости от касательных напряжений, что одно и то же) и наоборот. Эксперименты хорошо подтверждают эти предположения. Забегая вперед, отметим, что прочность напротив сильно зависит от сочетания касательных и нормальных напряжений.
Примечание: Приведенные выше законы и предположения подтверждаются многочисленными прямыми и косвенными экспериментами, но, как и все другие законы, имеют ограниченную область применимости.
Дата добавления: 2015-08-11; просмотров: 717;
