Плотность тока термоэмиссии

Важнейшей экспериментально наблюдаемой характеристикой является плотность тока эмиссии j. По физическому смыслу величина j есть количество электрического заряда, переносимого в единицу времени через единицу площади границы эмиссии или границы раздела металл-вакуум. Граница эмиссии понимается в том смысле, в каком мы ее обсуждали в § 2 и § 3. Аналитически j определяется выражением

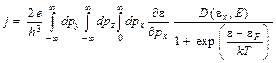(4.1)

, интегрирование по dp_y dp_z проводится в плоскости, компланарной плоскости эмиссии p_х , и e_x  импульс и энергия движения, нормального по отношению к плоскости эмиссии, e  полная энергия электрона в металле, e_F  энергия Ферми, Т  температура в °К, k  постоянная Больцмана.

Дадим пояснения к формуле (4.1). Произведение Df, где , есть произведение вероятностей двух независимых событий, вероятности туннелирования D частицы на вероятность f иметь энергию e . Другими словами, произведение Df есть функция распределения или фазовая плотность эмиттирования электронов справа от барьера (см. рис. 2.5). При учете (3.13)(3.19) , т.е. это скорость, с которой частица пересекает границу эмиссии. Произведение фазовой плотности на скорость и на заряд е дает плотность тока в фазовом пространстве. Суммирование по всем возможным значениям импульса дает наблюдаемую плотность тока в реальном трехмерном пространстве. Суммирование в (4.1) заменено на интегрирование согласно правилам (1.4)(1.5).

Интегрирование по dp_x проводится в пределах от нуля до бесконечности, поскольку пересекать границу эмиссии могут только те электроны, которые двигаются слева направо. Интегрирование по dp_y и dp_z проводится по всем значениям, поскольку эмиттировать частица может с любым значением составляющей импульса, лежащей в плоскости эмиссии. Размерность плотности тока есть произведение заряда на концентрацию и на среднюю дрейфовую скорость 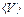, т.е. j = en 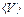. В дальнейшем, так, как это принято в эмиссионной электронике, будем называть металлический образец, из которого эмиттируют электроны, эмиттером или катодом. Электрическое поле реализуется в системах, состоящих из двух металлических электродов, разделенных вакуумным промежутком, к которым приложена разность потенциалов. Отрицательный электрод называется катодом, положительный - анодом или коллектором. При записи (4.1) предполагалось, что распределение по энергиям электронов в зоне проводимости катода описывается функцией Ферми-Дирака, а наибольшие отклонения от этой функции распределения, связанные с явлениями переноса, дают пренебрежимо малый вклад в ток эмиссии. При вычислении (4.1) используются два подхода. NED-представление (“Normal Energy Distribution”  распределение по нормальным энергиям), и TED-представление (“Total Energy Distribution”  распределение по полным энергиям ). Оба этих подхода оказываются полезными при анализе явления эмиссии, поэтому продемонстрируем их.

NED-представление

Вычисления будем проводить в рамках модели свободных электронов. Ниже мы обсудим правомочность такого приближения. Делаем замену переменных согласно схеме

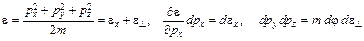, (4.2)

тогда

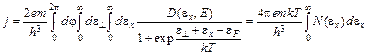, (4.3)

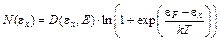, (4.4)

N( 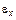)  функция распределения по нормальным энергиям эмиттированных электронов.

TED-представление

Делаем замену переменных интегрирования

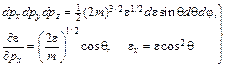, (4.5)

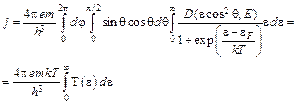, (4.6)

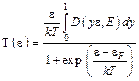, (4.7)

Т(e)  функция распределения по полным энергиям эмитированных электронов. Учитывая важность функций N(e_x) и Т(e) при определении термоавтоэмиссионных характеристик катода, исследуем их отдельно.