Коэффициент прозрачности
Основной количественной характеристикой процесса туннелирования является коэффициент прохождения частицы через потенциальный барьер или коэффициент прозрачности D. Пусть частица падает на потенциальный барьер, двигаясь вдоль оси х слева направо. Ее полная энергия меньше максимума потенциальной. На рис. 3.1 схематически изображено прохождение частицы через барьер. В области I волновая функция частицы имеет осциллирующий характер и состоит из падающей и отраженной волны, в области II экспоненциально затухает, и в области III опять осциллирует с гораздо меньшей амплитудой и состоит только из прошедшей волны. Длина стрелок на рис. 3.1 пропорциональна плотности потока вероятности, соответственно падающего, отраженного и прошедшего, определяемого в квантовой механике как
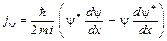, (3.1)
где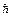 
= h/2p, i мнимая единица, y* комплексно сопряженная волновая функция. Коэффициент прозрачности определяется как отношение величин прошедшей плотности потока вероятности к падающей
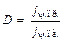. (3.2)
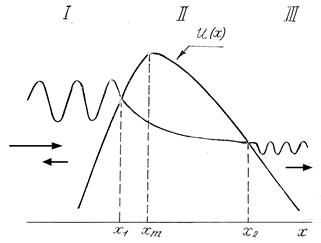
Рис. 3.1
В квантовой механике решена задача о прохождении частицы через потенциальный барьер в квазиклассическом приближении, и найден коэффициент прозрачности
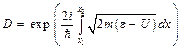, (3.3)
х1 и х2 точки поворота, в которых полная энергия e становится равной потенциальной, а импульс частицы равным нулю. Квазиклассическое приближение накладывает ряд условий, при которых справедлив результат (3.3).
1. Потенциальный барьер достаточно широк и
D = 1 (3.4)
2. Длина волны де Бройля частицы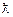 
достаточно мала.
3. Достаточно медленно изменяется потенциальная энергия U, так, что на длине порядка 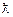мало изменение импульса частицы.
Аналитически два последних условия запишутся в виде
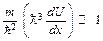, (3.5)
где
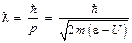. (3.6)
Перечисленные ограничения означают, что квазиклассическое приближение и формула (3.3) становятся неприменимыми вблизи вершины барьера и вблизи точек поворота. Кембл решил точно, без квазиклассического приближения, задачу о прохождении частицы через потенциальный барьер параболической формы. Для системы координат, соответствующей рис. 3.1, параболический барьер можно представить в виде
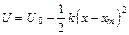(3.7)
и задача о прохождении через барьер сводится к задаче о линейном осцилляторе, решение которой хорошо изучено. Кэмбл получил точное выражение для коэффициента прозрачности
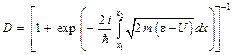(3.8)
справедливое при любых значениях энергии e. Действительно, если энергия меньше вершины барьера, что соответствует подбарьерному прохождению частицы, то значения координат точек поворота х1 и х2 вещественны, подкоренное выражение в (3.8) отрицательное и показатель экспоненты положительное вещественное число. Если энергия больше вершины барьера и имеет место надбарьерное прохождение, то значения координат точек поворота комплексные величины, подкоренное выражение положительное и показатель экспоненты в (3.8) отрицательное вещественное число. По мере того, как энергия превышает вершину барьера, отрицательный вещественный показатель экспоненты очень быстро растет по модулю и коэффициент прозрачности становится равным единице. В случае подбарьерного прохождения при достаточном удалении от вершины барьера по энергии формула (3.8) переходит в (3.3).
Достаточно гладкий барьер произвольной формы можно вблизи вершины аппроксимировать формулой (3.7). Это наводит на мысль, что формулу (3.8) можно использовать для произвольных барьеров. Миллер и Гуд проанализировали это обстоятельство и показали, что формула (3.8) с хорошей точностью описывает произвольные гладкие барьеры с максимумом. Эту формулу мы и будем использовать в своих дальнейших вычислениях.
Обратимся теперь к нашему конкретному барьеру на границе металл-вакуум при наличии тянущего электроны электрического поля (см. рис. 3.2). Координаты точек поворота находятся из уравнения
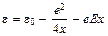, (3.9)
откуда
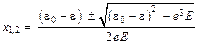. (3.10)
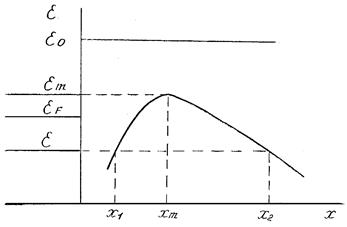
Рис. 3.2
Если (e0 e) > (е3Е)1/2(подбарьерное прохождение, как показано на рис. 3.2), то х1 и х2 имеют два различных вещественных значения, при надбарьерным прохождением (e0 e) < (е3Е)1/2и х1 и х2 комплексные величины. При e = em или
e0 e = (е3Е)1/2 х1 = х2 = хm из (2.10) (прохождение с рассеянием на вершине барьера). Подстановка потенциала сил изображения в (3.8) дает следующее выражение для коэффициента прозрачности
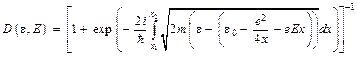. (3.11)
Интеграл в (3.11) через элементарные функции не выражается. Результат вычисления D(e, Е) можно представить в виде
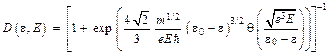, (3.12)
где функция q(у) называется функцией Нордгейма, она выражается через эллиптические интегралы и для нее составлены таблицы.
Выше, при рассмотрении задачи о коэффициенте прозрачности мы предполагали, что движение частицы носит одномерный характер, т.е. частица имеет одну степень свободы и соответственно импульс вдоль оси х, перпендикулярной барьеру. На самом же деле электрон в металле и вне его имеет три степени свободы и соответствующие компоненты импульса и энергии
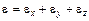, (3.13)
где
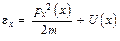, (3.14)
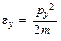, (3.15)
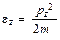. (3.16)
Энергия eх(х) не зависит от координаты х, т.к. согласно уравнению движения
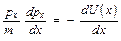(3.17)
и
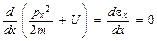, (3.18)
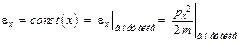. (3.19)
Из предыдущих рассуждений ясно, что процесс туннелирования зависит только от величины eх, а движение в плоскости, компланарной границы эмиссии, не оказывает влияние на прохождение частицы через потенциальный барьер. В формулы (3.3), (3.6), (3.8), (3.12) необходимо подставлять в качестве аргумента eх, т.е. D = D(eх, Е).
Дата добавления: 2015-08-11; просмотров: 1122;