Дополнение 2

Формула (2.7) справедлива при х 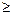а, где а  постоянная решетки. Это означает, что поля ограничены сверху таким образом, чтобы левая точка поворота, соответствующая заметной эмиссии с данной энергией, х₁ 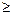а. Иногда используют модифицированную формулу для потенциального барьера

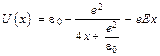. (Д2.1)

Замена 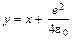сводит (Д2.1) к потенциалу (2.7). При этом энергия 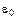увеличивается на величину 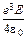, что приводит к увеличению на ту же величину работы выхода в конечных формулах эмиссии. При сильных полях, когда возможно наблюдение отклонения от потенциала сил изображения, может иметь место эффект проникновения поля в металл. Этот эффект приводит к понижению работы выхода, что компенсирует увеличение работы выхода за счет отклонения от потенциала сил изображения вплоть до полей Е 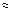10⁸В/см.

Необходимо заметить следующее. Формулы (2.7) и (Д2.1) подразумевают, что металл обладает идеальной электропроводностью, т.е. “дырка” изображения успевает занять положение, зеркальное по отношению к эмиттированному электрону. Реальный металл обладает конечной электропроводностью и некоторой высокочастотной диэлектрической проницаемостью. В результате реальная работа выхода может отличаться от величины 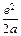для идеального случая, причем это отличие состоит из двух частей: обратимой, связанной с отставанием “дырки” от идеального изображения, а также необратимой, связанной с джоулевой диссипацией токов, образующих “дырку”. Точная количественная теория этого эффекта сложна, но, на наш взгляд, оценить влияние этого эффекта можно, если переписать формулу (Д2.1) в виде

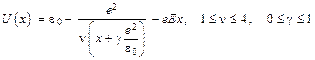. (Д2.2)

Выше мы пользовались представлениями об одномерном барьере, т.е. предполагали, что граница металл-вакуум является идеальной плоскостью. Такая картина далека от действительности, поскольку реальная поверхность твердого тела обладает тангенциальной периодичностью, а также нарушениями ее. То есть в общем случае необходимо решать трехмерную задачу. Эта задача очень сложна и решения до сих пор не получено. Следует, однако, заметить, что, по-видимому, влияние указанных эффектов станет существенным, когда ширина барьера будет сравнима с размерами тангенциальных неоднородностей х₂  х₁ а.