Алгебраическое дополнение.
Поставим в соответствие каждому элементу матрицы (1.1) некоторое число – его алгебраическое дополнение.
Алгебраическим дополнением 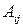 элемента
элемента 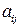 матрицы
матрицы 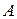 называется определитель
называется определитель 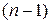 -го порядка, получаемый из вычеркиванием
-го порядка, получаемый из вычеркиванием 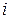 -й строки и
-й строки и 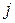 -го столбца, взятый со знаком «+», если сумма
-го столбца, взятый со знаком «+», если сумма 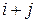 четная, и со знаком «–», если эта сумма нечетная.
четная, и со знаком «–», если эта сумма нечетная.
Пример 1.4а. Найти алгебраические дополнения к элементам матрицы второго порядка.
Решение. Запишем матрицу в общем виде:  . Тогда
. Тогда 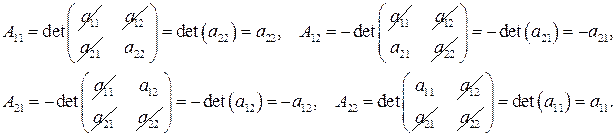
Пример 1.4б. Найти алгебраические дополнения к элементам первой строки матрицы 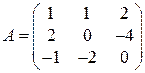 .
.
Решение.

Свойства определителей. (Здесь и далее строки и столбцы в общем будем называть рядами.)
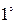 . При перестановке двух параллельных рядов определитель меняет знак.
. При перестановке двух параллельных рядов определитель меняет знак.
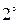 . Определитель, содержащий два пропорциональных ряда, равен нулю.
. Определитель, содержащий два пропорциональных ряда, равен нулю.
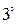 . Общий множитель элементов какого-либо ряда можно вынести за знак определителя.
. Общий множитель элементов какого-либо ряда можно вынести за знак определителя.
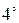 . Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на одно и то же число.
. Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на одно и то же число.
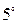 . (Правило своих дополнений.) Определитель равен сумме произведений элементов любого ряда на их алгебраические дополнения.
. (Правило своих дополнений.) Определитель равен сумме произведений элементов любого ряда на их алгебраические дополнения.
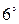 . (Правило чужих дополнений.) Сумма произведений элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
. (Правило чужих дополнений.) Сумма произведений элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
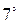 .
. 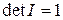 .
.
 .
. 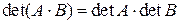 .
.
Пример 1.5а. Используя правило своих дополнений, вычислить определитель матрицы 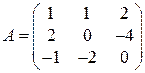 .
.
Решение. Применим свойство 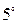 , например, к первой строке:
, например, к первой строке: 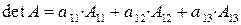 . С учетом результатов примера 1.4б, получим:
. С учетом результатов примера 1.4б, получим:
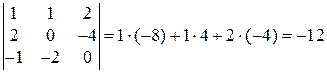 .
.
Дата добавления: 2015-07-18; просмотров: 2403;
