Матричный метод
Рассмотрим квадратную (число уравнений равно числу неизвестных), невырожденную (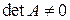 
) СЛАУ 
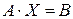. При указанных условиях существует матрица, обратная к 
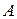. Чтобы найти неизвестную 
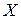, умножим обе части слева на 
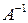. Тогда
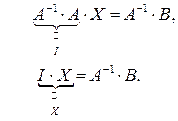
Отсюда получим формулу для отыскания :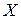
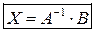
Пример 1.7. Решить СЛАУ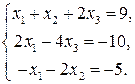 
Решение. Обозначим
.
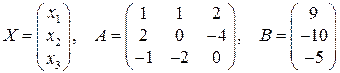Для отыскания 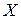можно применить полученную выше формулу, т.к. основная матрица системы 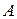– квадратная, и ее определитель – основной определитель – 
(см. пример 1.6). Таким образом
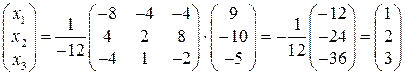
(матрица 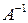была найдена в примере 1.6).
Ответ: 
.
Убедимся в правильности результата – подставим в каждое уравнение системы:
.
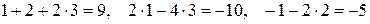Все уравнения обратились в тождества, что и требовалось доказать.
Замечание. Ответ к задаче можно дать в другом виде: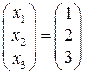 
или просто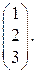 
Дата добавления: 2015-07-18; просмотров: 1014;