Метод Гаусса. где , не обязательно равно , а в случае не обязательно отличен от нуля.

Рассмотрим систему (1.4)

,

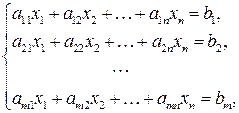где 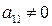, 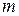не обязательно равно 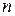, а в случае 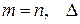не обязательно отличен от нуля.

Суть метода Гаусса – последовательный переход от исходной системы к эквивалентной ей «треугольной » системе

,

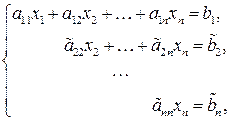которая без труда решатся методом подстановки .

Всю информацию о системе содержит так называемая расширенная матрица СЛАУ, она имеет вид:

.

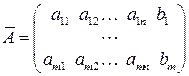Будем выделять прямой и обратный ход метода Гаусса.

I. Прямой ход. Элементарными преобразованиями над строками приводим расширенную матрицу системы к «трапециевидной».

II. Обратный ход. По последней матрице восстанавливаем СЛАУ, которая, очевидно, эквивалентна исходной, и приводим ее к треугольному виду. Решаем ее методом подстановки «снизу вверх».

Пример 1.9. Решить СЛАУ методом Гаусса

1.9а.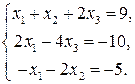

Решение.

I. Прямой ход.

II. Обратный ход.

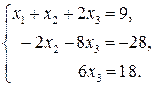
Эта система была решена в (см. пример 1.8).

Ответ:

1.9б.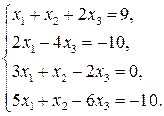

Решение.

I. Прямой ход.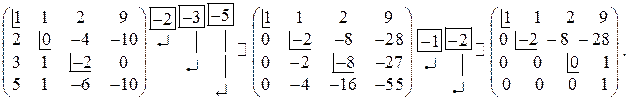

II. Обратный ход.

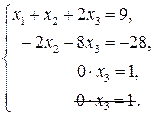
Третье и четвертое уравнения одинаковые, и мы вычеркнули одно из них:

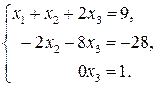
Последнее уравнение не имеет решений, значит, и вся система не имеет решения.

Ответ: система несовместна.

1.9в.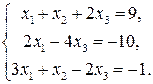

Решение.

I. Прямой ход.

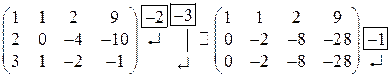
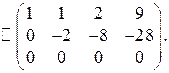
II. Обратный ход.

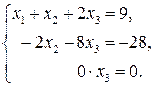
Последнему уравнению удовлетворяет любое действительное число, обозначим 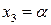. Выражая последовательно из второго уравнения :

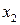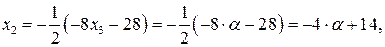
а затем из третьего – :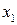

,

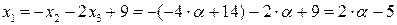получим бесконечное множество решений.

Ответ: .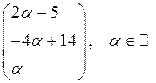

1.9г.

Решение.

I. Прямой ход.

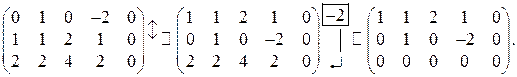
II. Обратный ход.

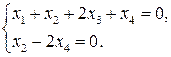
Чтобы привести систему к треугольной, внесем в нее два тождества :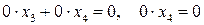

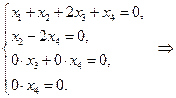
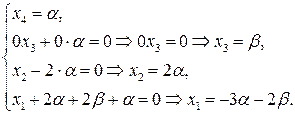
Ответ:

Замечания:

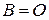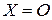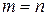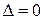- Однородная система, т.е. система (1.4), где , всегда совместна. Она имеет как минимум одно решение , так называемое тривиальное решение. В частности, при и – однородная СЛАУ имеет нетривиальные решения.

- При решении однородных систем столбец свободных членов после элементарных преобразований не меняется, поэтому достаточно преобразовывать основную матрицу системы.