Линейные операции над векторами
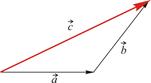
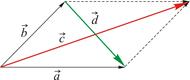
 Пусть начало вектора Пусть начало вектора 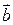 совпадает с концом вектора совпадает с концом вектора 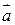 . Суммой векторов . Суммой векторов 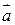 и и 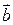 будем называть вектор, соединяющий начало вектора будем называть вектор, соединяющий начало вектора 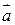 с концом вектора с концом вектора 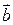 . .
| 
|
 Разностью векторов Разностью векторов 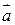 и и 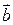 называется вектор называется вектор 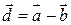 такой, что такой, что 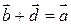 . .
| 
|
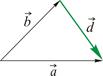
Правило параллелограмма. Сумма векторов 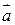 и и 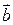 – диагональ построенного на них параллелограмма, идущая из их общего начала. Разность – диагональ построенного на них параллелограмма, идущая из их общего начала. Разность 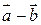 – вторая диагональ, идущая к уменьшаемому – вторая диагональ, идущая к уменьшаемому
| 
|
 При умножении вектора
При умножении вектора
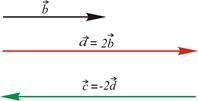 - на положительное число
- на положительное число 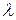 его длина увеличивается в
его длина увеличивается в 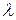 раз, направление не меняется;
раз, направление не меняется;
- на отрицательное число 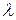 его длина увеличивается в
его длина увеличивается в 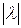 раз, направление меняется на противоположное;
раз, направление меняется на противоположное;
- на ноль – получаем нуль-вектор (направление не определено).
Дата добавления: 2015-07-18; просмотров: 817;
