Модуль вектора. Направляющие косинусы. Орт вектора
Зная координаты вектора в ДСК
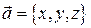 ,
можно найти его модуль как длину диагонали прямоугольного параллелепипеда: ,
можно найти его модуль как длину диагонали прямоугольного параллелепипеда:
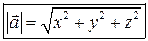 .
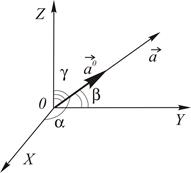
Пусть углы вектора с осями .
Пусть углы вектора с осями 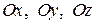 соответственно равны соответственно равны 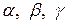 .
По свойству проекции .
По свойству проекции  имеем: имеем:
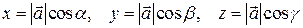 ,
или ,
или
| 
|
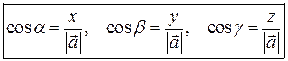
Из приведенных выражений нетрудно получить:
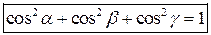 .
.
Обозначим орт вектора 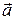 (вектор, имеющий то же направление и единичную длину) через
(вектор, имеющий то же направление и единичную длину) через 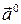 . Очевидно
. Очевидно
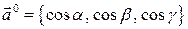 или
или 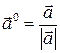 .
.
Дата добавления: 2015-07-18; просмотров: 1332;
