Приложения векторного произведения
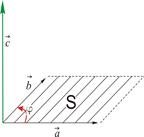
1. Площадь параллелограмма, построенного на векторах 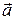 и и 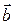 , равна , равна 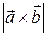 . .
| 
|
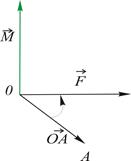
2. Момент силы 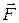 , приложенной к точке , приложенной к точке 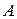 , относительно точки , относительно точки 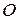 равен равен 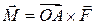 . .
| 
|
Пример 2.3. Найти векторное произведение векторов 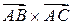 , если известны координаты точек
, если известны координаты точек 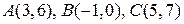 .
.
Решение. Сначала найдем координаты векторов по правилу «конец минус начало»:
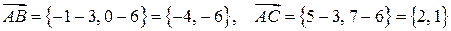 . Далее возможны два способа решения.
. Далее возможны два способа решения.
I способ. Запишем векторы в виде 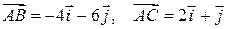 и, с учетом свойств
и, с учетом свойств 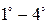 получим:
получим:
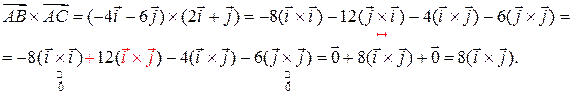
Всем пунктам определения векторного произведения 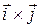 отвечает вектор
отвечает вектор 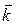 , таким образом
, таким образом 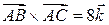 .
.
II способ. Векторы 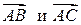 заданы в базисе
заданы в базисе 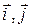 . Если ввести третью координату (например, 0), то можно найти их векторное произведение, пользуясь свойством
. Если ввести третью координату (например, 0), то можно найти их векторное произведение, пользуясь свойством 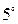 :
:
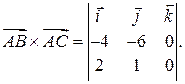
Определитель в правой части
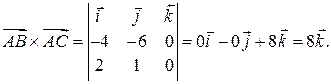
Ответ: 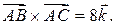
Дата добавления: 2015-07-18; просмотров: 1232;
