Разложение вектора по декартову базису. Координаты вектора
Декартовой системой координат (ДСК) в пространстве называется тройка попарно перпендикулярных числовых осей с общим началом и одинаковой единицей масштаба. Обозначим 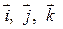 – орты координатных осей (координатные орты).
Декартовым базисом в пространстве будем называть тройку попарно перпендикулярных ортов. Задание ДСК равносильно заданию декартова базиса – орты координатных осей (координатные орты).
Декартовым базисом в пространстве будем называть тройку попарно перпендикулярных ортов. Задание ДСК равносильно заданию декартова базиса
| 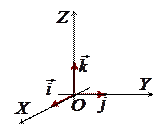 рис рис
|
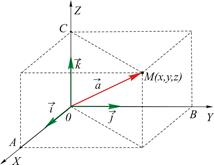 Пусть в пространстве задана ДСК и произвольный вектор
Пусть в пространстве задана ДСК и произвольный вектор 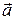 , причем его начало совпадает с началом координат.
, причем его начало совпадает с началом координат.
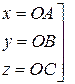 – проекции вектора на оси координат.
– проекции вектора на оси координат.
Из рисунка имеем:
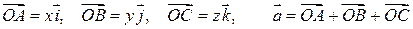 или
или
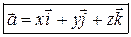
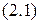
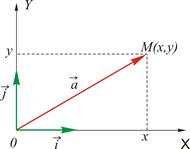 Таким образом доказано: если в пространстве задан декартов базис, то любой вектор может быть представлен в виде суммы
Таким образом доказано: если в пространстве задан декартов базис, то любой вектор может быть представлен в виде суммы 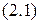 , где
, где  – проекции вектора на координатные оси. Формула
– проекции вектора на координатные оси. Формула  называется разложением вектора по базису
называется разложением вектора по базису 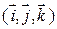 , числа
, числа 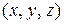 – координаты вектора
– координаты вектора 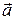 в данном базисе.
в данном базисе.
Замечание. На плоскости справедливо представление вектора в виде
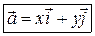 или
или 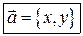 .
.
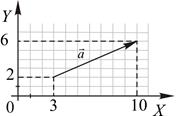
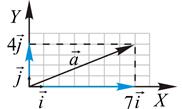
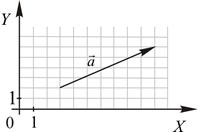 Пример 2.1. Найти координаты вектора
Пример 2.1. Найти координаты вектора 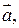 приведенного на рисунке.
приведенного на рисунке.
Решение.
I способ. Найдем проекции вектора на координатные оси: 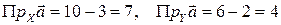 . Следовательно, . Следовательно, 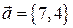 . .
| 
|
II способ. Параллельным переносом вектора совмести его начало с началом координат. Нетрудно убедиться, что согласно правилу параллелограмма, вектор 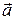 равен сумме векторов равен сумме векторов 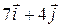 . .
| 
|
Теорема. Линейные операции над векторами сводятся к таким же операциям над их одноименными координатами:
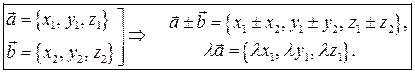
Доказательство. Пусть 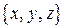 – координаты вектора
– координаты вектора  в данном базисе. Тогда
в данном базисе. Тогда  :
:

Остальное ( 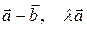 ) доказывается аналогично.
) доказывается аналогично.
В частности, 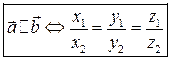 .
.
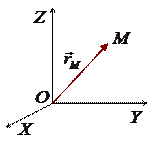
Правило «конец - начало»
рисРадиус-вектором точки  называется вектор, идущий из начала координат в данную точку: называется вектор, идущий из начала координат в данную точку:
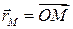 .
Координаты точки будем называть координаты ее радиус-вектора. .
Координаты точки будем называть координаты ее радиус-вектора.
| 
|
Справедливо утверждение
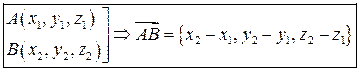
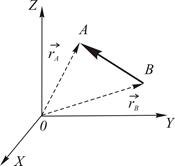
Доказательство.
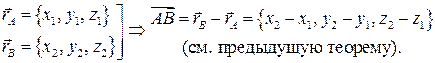
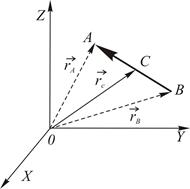 Пример 2.2. Даны координаты концов отрезка
Пример 2.2. Даны координаты концов отрезка 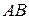 :
: 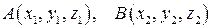 и некоторое число
и некоторое число 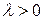 .
.
На отрезке 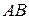 найти: координаты точки
найти: координаты точки 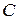 такой, что
такой, что 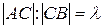 .
.
Решение.
Обозначим координаты искомой точки 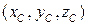 . Тогда
. Тогда
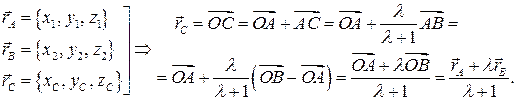
Таким образом 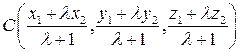 .
.
В частном случае, при 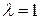 (деление отрезка пополам), имеем
(деление отрезка пополам), имеем
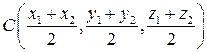 .
.
Дата добавления: 2015-07-18; просмотров: 5440;
