Обратная матрица.

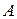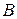Матрицы и называются взаимно обратными, если 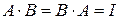. При этом будем обозначать .

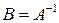Теорема.Обратная матрица 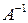существует тогда и только тогда, когда 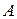– квадратная и 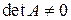(так называемая невырожденнаяматрица). При этом

.

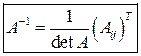Доказательство. 1. Чтобы выполнялось равенство 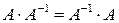, матрица 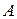должна быть квадратной (см. замечание к пункту ).

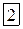2. Пусть 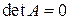и при этом существует 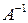. Тогда 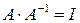, и, очевидно, должно выполняться равенство 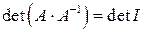. Используя свойства и 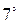определителей, получим:

.

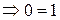Пришли к противоречию, значит, если 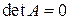, то 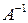не существует.

3. Формулу для нахождения обратной матрицы докажем на примере матрицы 2-го порядка (см. пример 1.4 а).

.

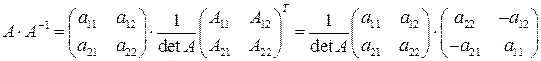
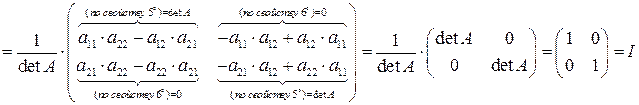Аналогично доказывается равенство .

Пример 1.6. Найти матрицу, обратную матрице .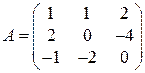

Решение. Согласно теореме для матрицы 3-го порядка .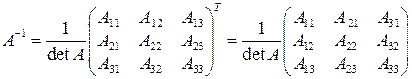

Из результатов примеров 1.5а, 1.4б имеем:

.

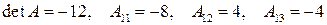Алгебраические дополнения к остальным элементам матрицы равны: .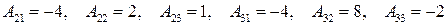

Ответ: .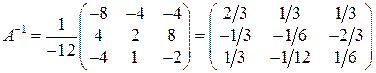

§ 2. Системы линейных алгебраических уравнений

Основные понятия

Системой линейных алгебраических уравнений (СЛАУ) называется система вида

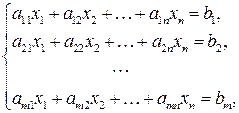(1.4)

где числа 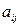– коэффициенты системы, 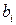– свободные члены, 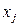– неизвестные (подлежат нахождению).

Решением системы (1.4) называется 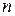значений неизвестных 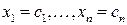, при подстановке которых все уравнения системы обращаются в верные равенства.

Известно, что СЛАУ может

-не иметь решений (система называется несовместной);

-иметь единственное решение (система называетсяопределенной);

-иметь бесконечное множество решений (система называется неопределенной).

Решить систему – значит найти все ее решения или доказать, что она несовместна.

Систему (4) можно записать в виде

.

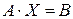Здесь 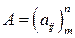- основнаяматрица системы,

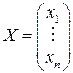– столбец неизвестных, 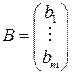– столбец свободных членов.

Приведем некоторые метода решения СЛАУ.