Определитель.

Каждой квадратной матрице по определенному правилу можно поставить в соответствие некоторое число – определитель (или детерминант) матрицы.

Пусть дана квадратная матрица порядка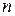

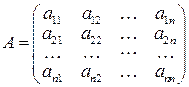. (1.1)

Рассмотрим произведения 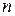элементов этой матрицы таких, что каждая строка и каждый столбец имеют в них по одному представителю:

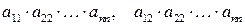и т.д.

Такие произведения в общем виде могут быть записаны

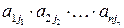. (1.2)

Здесь первые индексы (номера строк) расположены по возрастанию, вторые (номера столбцов)

(1.3)

образуют перестановку из 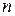чисел.

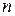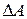Определителемматрицы -го порядка (1.1) называется сумма произведений вида (1.2), взятых со знаком «+», если перестановка (1.3) четная, и со знаком «–» – в противном случае. (Определитель будем обозначать или или 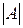.) Порядком определителя будем считать порядок соответствующей ему матрицы.

Приведем формулы для вычисления определителей 1, 2, и 3 –го порядков:

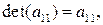
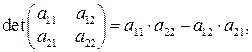
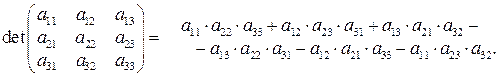
Пример 1.3. Вычислить определитель матрицы .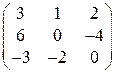

Решение.