Определитель. Действия над квадратными матрицами

Введем необходимые для дальнейшего изложения определения четных и нечетных перестановок..

Расположение чисел 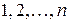в каком-либо порядке называются перестановкой. Число перестановок из 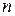чисел равно 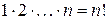( 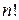читается «эн-факто-риал» – произведение первых 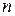натуральных чисел).

Рассмотрим перестановку 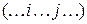. Если 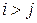, то говорят, что пара 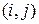образует инверсию. Перестановка называется четной, если она содержит четное число перестановок, и нечетной– в противном случае.

Из чисел 1, 2, 3 , например, существует 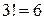перестановок:

1 2 3, 1 3 2, 2 1 3, 2 3 1, 3 1 2, 3 2 1.

При этом 1 2 3 – четная, т.к. в ней нет (ноль) инверсий, 2 1 3 – нечетная, т.к. содержит одну инверсию (2,1).