Числовые множества.
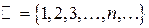 – множество натуральных чисел;
– множество натуральных чисел;
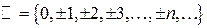 – множество целых чисел;
– множество целых чисел;
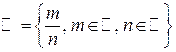 – множество рациональных чисел;
– множество рациональных чисел;
I – множество иррациональных чисел – нерациональные числа, которые можно представить в виде бесконечной непериодической десятичной дроби;
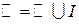 – множество действительных чисел.
– множество действительных чисел.
Числовые промежуткипредставляют собой подмножества множества  :
:
отрезок 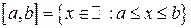 ;
;
интервал 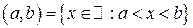 ;
;
полуинтервалы 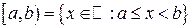 ,
, 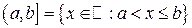 ;
;
бесконечные промежутки 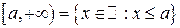 ,
, 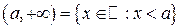 ,
, 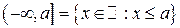 ,
, 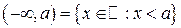 ,
, 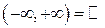 .
.
III. Основные алгебраические соотношения
Действия со степенями и логарифмами
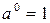
| 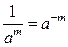
| 
| 
|
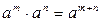
| 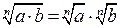
| 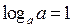
| 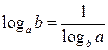
|

| 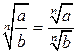
| 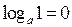
| 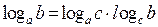
|
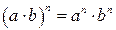
| 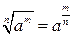
| 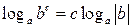
| 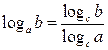
|
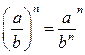
| 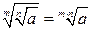
| 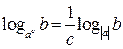
| 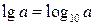
|
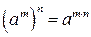
| 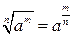
| 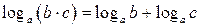
| 
|
Формулы сокращенного умножения
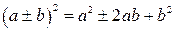
| 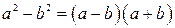
|
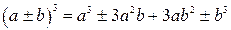
| 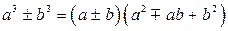
|
Корни квадратного уравнения 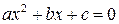
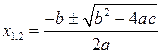
|
Разложение квадратного трехчлена на множители
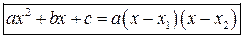 , где
, где 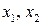 – корни уравнения
– корни уравнения 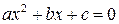 .
.
Выделение полного квадрата в квадратном трехчлене
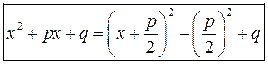 .
.
IV. Основные тригонометрические соотношения рис
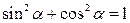
| 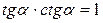
| 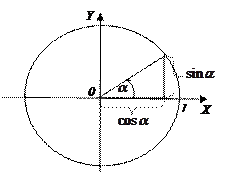
|
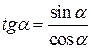
| 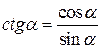
| |
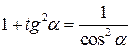
| 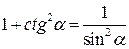
| |
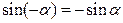
| 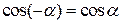
|
Сумма и разность двух аргументов
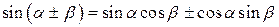
| 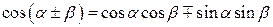
|
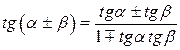
| 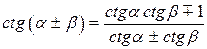
|
Двойные аргументы
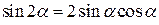
| 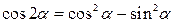
| 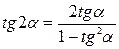
| 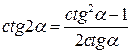
|
Формулы понижения степени
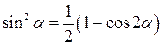
| 
|
Преобразование произведения в сумму
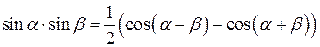
| 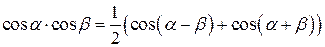
|
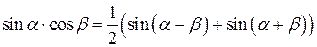
|
Преобразование суммы и разности в произведение
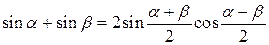
| 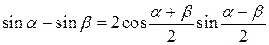
|
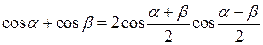
| 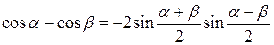
|
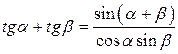
| 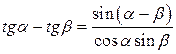
|
Некоторые значения тригонометрических функций
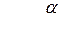
| 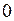
| 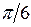
| 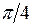
| 
| 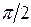
| 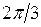
| 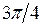
| 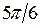
| 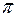
|
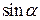
| 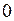
| 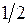
| 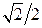
| 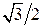
| 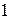
| 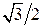
| 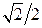
| 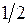
| 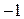
|
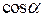
| 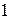
| 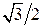
| 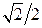
| 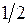
| 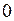
| 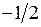
| 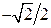
| 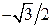
| 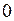
|

| 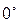
| 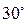
| 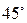
| 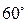
| 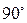
| 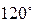
| 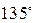
| 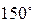
| 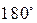
|
Тригонометрические уравнения
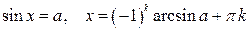
| 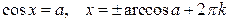
|
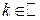
|

| 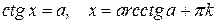
|
Раздел 1. ЛИНЕЙНАЯ АЛГЕБРА
§1. МАТРИЦЫ
Основные понятия. Сложение, вычитание, произведение матрицы на число, произведение матриц
Числовой матрицей называется квадратная или прямоугольная таблица чисел. Общая форма записи
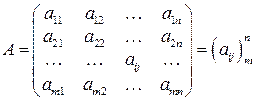 .
.
Здесь
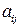 – элемент матрицы, стоящий на пересечении
– элемент матрицы, стоящий на пересечении 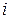 - й строки и
- й строки и 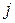 - го столбца;
- го столбца;
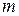 – число строк,
– число строк, 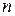 – число столбцов;
– число столбцов; 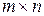 – размер матрицы.
– размер матрицы.
Например, матрица  имеет размер
имеет размер 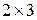 , а ее элемент, стоящий во второй строке и первом столбце
, а ее элемент, стоящий во второй строке и первом столбце 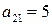 .
.
Матрица, все элементы которой равны нулю, называется нуль-матрицей:
 .
.
В случае 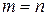 матрица называется квадратной порядка
матрица называется квадратной порядка 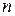 , ее элементы
, ее элементы 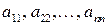 – составляют главную диагональ.
– составляют главную диагональ.
Квадратная матрица, главная диагональ которой состоит из «1», а остальные элементы – «0» называется единичной:
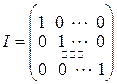 .
.
Линейные операции (сложение, вычитание, умножение на число) выполняются поэлементно:
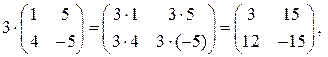
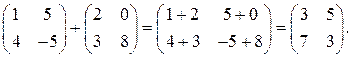
Сложение и вычитание матриц возможно, если они имеют одинаковый размер, т.е., например, невозможна операция
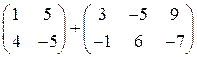 .
.
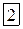 Произведение матрицы-строки
Произведение матрицы-строки 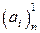 на матрицу-столбец
на матрицу-столбец 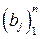 примем по определению:
примем по определению:
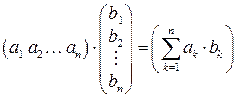 .
.
Знак 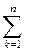 означает, что нужно суммировать стоящие под ним элементы, последовательно придавая в них индексу
означает, что нужно суммировать стоящие под ним элементы, последовательно придавая в них индексу 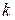 значения
значения 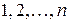 , т.е.
, т.е.
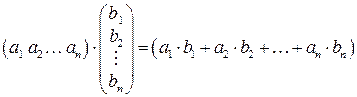 .
.
Произведение матрицы 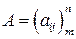 на матрицу
на матрицу 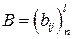 определим как матрицу
определим как матрицу 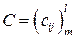 , каждый элемент
, каждый элемент 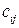 которой вычисляется по правилу умножения
которой вычисляется по правилу умножения 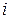 - ой строки матрицы
- ой строки матрицы 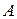 на
на 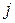 -й столбец матрицы
-й столбец матрицы 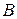 . (Формально
. (Формально 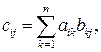
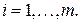 )
)
Пример 1.1. Найти матрицу 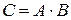 , если
, если 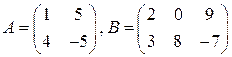 .
.
Решение.
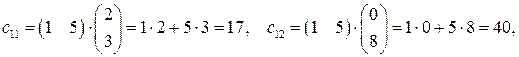
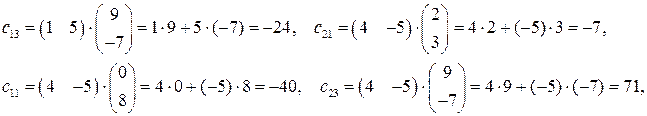
Ответ: 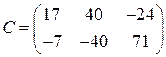 .
.
Замечания.
- умножение матриц выполнимо, если число столбцов первой матрицы равно числу строк второй (например, операция 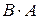 в условиях приведенного примера невозможна);
в условиях приведенного примера невозможна);
- вообще, 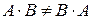 . Если
. Если 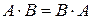 , такие матрицы называются перестановочными. (Докажите самостоятельно, что если матрицы перестановочны, то они квадратные.)
, такие матрицы называются перестановочными. (Докажите самостоятельно, что если матрицы перестановочны, то они квадратные.)
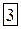 Матрица, получаемая из данной матрицы
Матрица, получаемая из данной матрицы 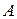 заменой строк столбцами с теми же номерами, называется транспонированнойк
заменой строк столбцами с теми же номерами, называется транспонированнойк 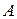 и обозначается
и обозначается 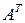 .
.
Например, транспонируя матрицу 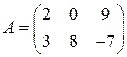 , получим:
, получим: 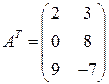 .
.
Свойства(при условии, что операции в обеих частях равенств выполнимы)
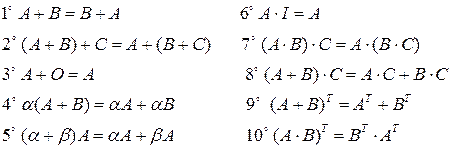
 Элементарными преобразованиями матрицы называются:
Элементарными преобразованиями матрицы называются:
- перестановка местами параллельных рядов;
- умножение ряда на ненулевое число;
- прибавление ко всем элементам ряда соответствующих элементов параллельного ряда, умноженных на одно и то же число (далее будем говорить кратко: прибавление к ряду параллельного ряда, умноженного на некоторое число).
Две матрицы 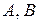 называются эквивалентными(обозначается
называются эквивалентными(обозначается 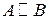 ), если одна из них получается из другой с помощью элементарных преобразований.
), если одна из них получается из другой с помощью элементарных преобразований.
Будем называть «трапециевидной» матрицу, у которой под элементами с одинаковыми индексами – нули:
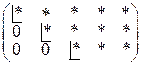 или
или 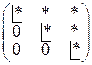 или
или 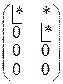 .
.
Пример 1.2. Элементарными преобразованиями над строками привести к «трапециевидной» матрицу 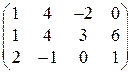 .
.
Решение. Чтобы обнулить соответствующие элементы в первом столбце, прибавим ко 2-й строке 1-ю, умноженную на (-1), и к 3-й строке –1-ю, умноженную на (-2):
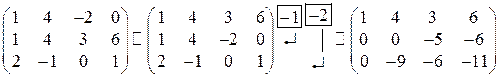 .
.
Осталось поменять местами 2-ю и 3-ю строки:
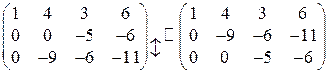 .
.
Таким образом,
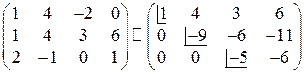 .
.
Дата добавления: 2015-07-18; просмотров: 1237;
