Энергетические распределения эмитированных электронов

Исследуем NED-распределение

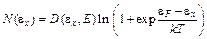. (5.1)

Качественный анализ функции N(e_х) показывает следующее (см. рис. 5.1) При Т®0 энергия эмитированных электронов в основном меньше e_F, максимум N( 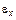) находится вблизи e_F и энергетический разброс определяется коэффициентом прозрачности D (рис. 5.1, а). При Е ® 0 энергия эмитированных электронов в основном больше e_m, максимум N( 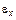) находится вблизи e_m, ширину распределения определяет функция 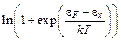(рис. 5.1, б). При конечных Е и Т максимум распределения по нормальным энергиям расположен между e_F и e_m (см. рис. 5.1, в). При увеличении Е прозрачность барьера растет и распределение сдвигается в сторону меньших энергий, с ростом Т  в сторону больших энергий.

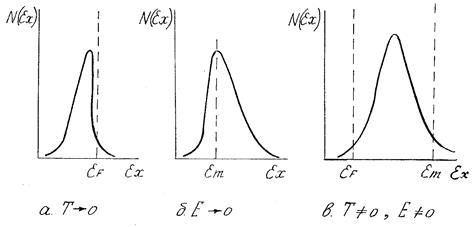
Рис. 5.1

Исследуем далее функцию N( 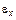) аналитически. При произвольных значениях напряженности электрического поля Е и температуры исследовать функцию N( 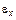) трудно, поскольку она имеет сложное математическое выражение из-за коэффициента прозрачности D( 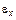, Е) (см. формулу (3.12). Поэтому прибегают к двум основным приближениям, которые представляют интерес с точки зрения физики и легко реализуются на практике.

1. Низкие температуры и высокие электрические поля (ЕТ эмиссия). Количественный критерий этого приближения будет дан ниже. Как уже указывалось, максимум N( 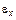) лежит вблизи e_F, поэтому показатель экспоненты (3.12) можно разложить около e_F в ряд Тейлора и ограничиться линейным слагаемым. Результат получается следующий:

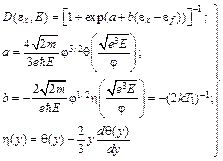. (5.2)

При записи (5.2) учтено определение работы выхода (2.8). Характеристическую температуру

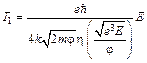(5.3)

называют температурой инверсии. Целесообразность введения этой величины и ее физический смысл станет понятен при вычислении плотности потока энергии через границу эмиссии, а пока отметим, что температура Т₁ линейно растет с напряженностью электрического поля Е и определяет ширину энергораспределения при низких температурах. Поскольку при низких температурах и высоких полях имеет место в основном подбарьерный выход электронов с катода, показатель экспоненты в формуле (5.2) для D достаточно велик

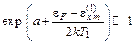(5.4)

и справедливо ВКБ-приближение (3.3). С учетом этого распределение по нормальным энергиям запишется в виде

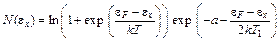. (5.5)

Из условия dN/d 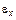= 0 находим уравнение для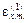

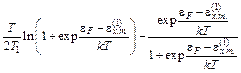. (5.6)

В силу всего сказанного выше естественно предполагать, что 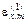< e_F, Т < Т₁ и

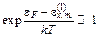. (5.7)

Пренебрегая в (5.6) единицей по сравнению с экспонентой, получаем

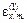= e_F  2kT. (5.8)

При подстановке результата (5.8) в условия (5.4) и (5.7) видно, что они выполняются. Максимальное значение N( 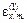) следующее

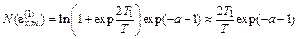. (5.9)

Для практических целей функцию N( 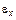) удобно отнормировать так, чтобы при она имела значение равное единице.

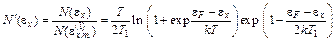(5.10)

Одной из экспериментально измеряемых характеристик является энергетическая ширина кривой N'( 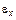) на полувысоте, т.е.

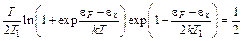(5.11)

Решение уравнения (5.11) относительно 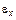даст правое 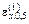и левое 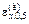значения корней и энергетическую ширину 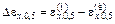(см. рис. 5.2). Трансцендентное уравнение (5.11) в общем случае необходимо решать численно.

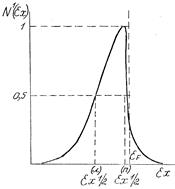
Рис. 5.2

2. Высокие температуры и слабые электрические поля (ТЕ эмиссия). В этом случае максимум N(e_х) лежит вблизи e_m и разложение, аналогичное (5.2) имеет вид

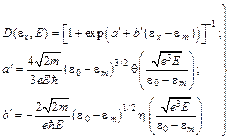. (5.12)

Для потенциала сил изображения: 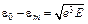, q(1) = 0, a' = 0,

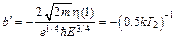. (5.13)

Вторая характеристическая температура

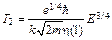(5.14)

не имеет явно выраженного физического смысла и специального названия, как температура инверсии Т₁, и служит в основном для удобства записи формул. Поскольку эмиссия происходит в энергетическом интервале, прилегающем к e_m, то в предположении e_m  e_F ? kT можно записать

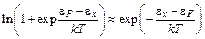. (5.15)

Подставляя (5.12)(5.15) в (5.1), получаем

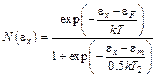. (5.16)

Условие dN/de_x = 0 приводит к уравнению

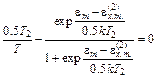. (5.17)

Решение этого уравнения дает

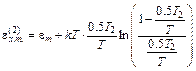(5.18)

и

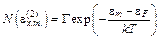, (5.19)

где

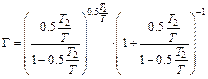. (5.20)

Отнормированное энергораспределение в данном случае

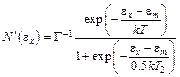. (5.21)

Аналогично (5.11), приравнивание выражения (5.21) 0,5 (??) дает возможность определить энергетическую ширину на полувысоте.

Исследуем далее TED-распределение

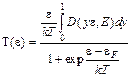. (5.22)

1. ЕТ эмиссия

Использование разложения (5.2) и условия (5.4) позволяет записать

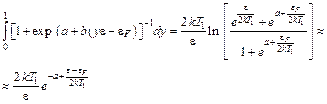(5.23)

и

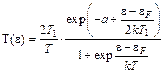
. (5.24)

Условие dT/de = 0 дает уравнение

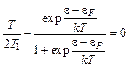, (5.25)

решение которого позволяет найти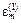

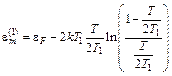(5.26)

Подстановка (5.26) в (5.24) приводит к формулам

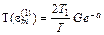(5.27)

и

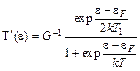, (5.28)

где

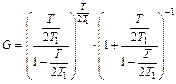. (5.29)

Энергетическая ширина ищется из уравнения

T'(e) = 1/2. (5.30)

2. ТЕ эмиссия

Используя разложение (5.12), можно записать

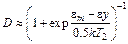(5.31)

и

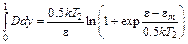, (5.32)

в предположении, что

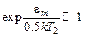. (5.33)

Подставляя (5.32) в (5.22) и используя приближение, аналогичное (5.15), получаем

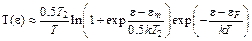. (5.34)

Условие максимума T(e) приводит к уравнению

. (5.35)

В данном случае естественно предположить, что

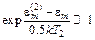, (5.36)

т.к. электроны несут энергию, соответствующую поперечным по отношению к направлению эмиссии степеням свободы (e  полная энергия). Тогда из (5.35) получаем

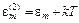, (5.37)

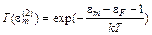, (5.38)

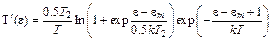. (5.39)

Приравнивание (5.38) (??) 0,5 определяет энергетическую ширину TED при высоких температурах и слабых электрических полях.