Элементы электронной теории металлов

Мурзакаев А.М.

ЛЕКЦИОННЫЕ МЕТОДИЧЕСКИЕ РАЗРАБОТКИ

по курсу "Физическая электроника"

для студентов дневной формы обучения

физического факультета

специальности –фундаментальная радиофизика и физическая электроника

Содержание

§ 1. Элементы электронной теории металлов. 3

Дополнение 1. 7

§ 2. Потенциальный барьер на границе металл-вакуум.. 7

Дополнение 2. 11

§ 3. Коэффициент прозрачности. 12

§ 4. Плотность тока термоэмиссии. 15

§ 5. Энергетические распределения эмитированных электронов. 16

§ 6. Плотность тока термоавтоэмиссии (продолжение) 22

§ 7. Плотность потока энергии через эмиссионную поверхность. 24

§ 8. Автоэлектронная эмиссия. Эксперимент. 25

8.1 Автоэмиттер. 25

8.2 Автоэмиссионный метод определения работы выхода. 26

8.3 Микроскопия поверхности твердого тела. 28

8.3.1 Автоэлектронная (полевая электронная) микроскопия. 29

8.3.2 Автоионная (полевая ионная) микроскопия. 31

8.3.3 Сканирующая туннельная микроскопия. 34

§ 9. Термоэлектронная эмиссия. 36

9.1 Термокатоды.. 36

9.2 Термоэмиссионный метод определения работы выхода. 37

§ 10. Другие виды электронной и ионной эмиссии. 38

10.1 Общая классификация явлений эмиссии. 38

10.2 Фотоэлектронная эмиссия (внешний фотоэффект) 39

10.3 Вторичная электронная эмиссия. 41

10.4 Кинетическая ионно-электронная эмиссия. 43

10.5 Экзоэлектронная эмиссия. 43

10.6 Потенциальная ионно-электронная эмиссия (потенциальное вырывание) 43

10.7 Эмиссия горячих электронов. 44

10.8 Комбинированные виды эмиссии. 44

§11. Токи, ограниченные пространственным зарядом.. 45

11.1 Закон «трех вторых». 45

11.2 Общая схема расчета самосогласованных полей и объемных зарядов 48

11.3 Плоскопараллельная электродная система. 50

11.4 Цилиндрическая электродная система. 53

11.5 Сферическая электродная система. 55

11.6 Влияние пространственного заряда на автоэлектронную эмиссию 55

§ 12. Взрывная электронная эмиссия (ВЭЭ) 57

12.1 Феноменология ВЭЭ.. 57

12.2 Импульсный пробой при острийном катоде. 58

12.3 Импульсный пробой при плоских электродах. 60

12.4 Пробой постоянным напряжением.. 61

12.5 Джоулев механизм вакуумного пробоя. 61

12.6 Вольт-амперная характеристика искрового разряда. 63

Литература. 65

Элементы электронной теории металлов

Макроскопическое твердое тело представляет систему из огромного числа частиц, взаимодействующих между собой. Для построения теории необходимы квантовомеханическое и статистическое описание и физическая модель твердого тела.

Модель включает следующие представления: твердое тело  это совокупность ионов и валентных электронов. Под ионами понимаются атомные ядра вместе с электронами заполненных оболочек. Взаимодействие этих электронов с ядром является столь сильным, что сближение атомов и образование кристалла не оказывает на них существенного влияния. И наоборот, при сближении ионов до расстояний порядка их собственных размеров валентные электроны данного атома вступают в сильное взаимодействие с соседними ядрами и их электронными оболочками. Это взаимодействие обеспечивает силы сцепления, образующие кристаллы. Валентные электроны уже нельзя считать локализованными у данного атома, они могут перемещаться по всему кристаллу, например, в случае металла. Их совокупность и образует систему электронов проводимости металла.

При построении теории пользуются целым рядом более или менее обоснованных допущений. Первое  это адиабатическое приближение. Ионы находятся в периодически расположенных узлах кристаллической решетки с расстоянием между ними , равным постоянной решетки a Это положение равновесия ионов. При конечных температурах за счет тепловой энергии они колеблются относительно своего положения равновесия. Валентные электроны также двигаются. В адиабатическом приближении считается, что легкие электроны движутся при заданных положениях тяжелых ионов, т.е. гораздо быстрее ионов. Каждому новому положению ионов отвечает свое распределение электронов, которые всегда успевают подстраиваться к изменившейся обстановке. Второе допущение касается взаимодействия между электронами проводимости металла по закону Кулона. Соответствующий анализ показывает, что отдельно взятый электрон проводимости движется окруженный положительно заряженной “шубой”. Положительный заряд “шубы” обусловлен зарядом ионов. Электрон проводимости при своем движении отталкивает другие электроны и вокруг него возникает движущийся вместе с ним некомпенсированный положительный ионный заряд. Движение электронов проводимости носит коллективный характер, каждый в своем движении влияет на других. Оказалось, что систему взаимодействующих электронов с массой m можно представлять как систему невзаимодействующих квазичастиц с эффективной массой m^* (квазичастица, образно говоря, это электрон плюс “шуба” с точки зрения инерции движения). В дальнейшем, в
целях упрощения и согласно принятой терминологии, квазичастицы мы будем называть электронами проводимости или просто электронами.

Третье допущение состоит в том, что электрон проводимости в кристалле представляется как свободная частица в потенциальной яме, как показано на рис. 1.1. Границы ямы обусловлены границами кристалла, глубина ямы  взаимодействием электронов и ионов. Это так называемое приближение квазисвободных электронов. Волновая функция электрона 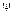, а также связь между его энергией e и импульсом p имеют вид:

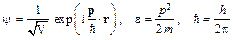, (1.1)

где h  постоянная Планка, 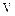 объём кристалла. Запись (1.1) является решением уравнения Шредингера для частицы в потенциальной яме, представленной на рис. 1.1, и удовлетворяет условию нормировки:

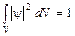. (1.2)

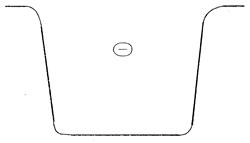
Рис. 1.1

Рассмотрим далее образование металла из невзаимодействующих атомов на примере простой модели. Пусть в атоме имеется один валентный электрон на соответствующем уровне энергии. Этот уровень будет двукратно вырожденным, поскольку энергия электрона не зависит от ориентации его спина. В системе, состоящей из N невзаимодействующих атомов соответствующий уровень будет 2N  кратно вырожден. При сближении атомов и установлении между ними взаимодействия, снимающего вырождение, уровень распадается на 2N уровней, образующих полосу. Половина этих уровней энергии будет занята парами электронов с противоположно направленными спинами, как это показано на рис. 1.2. Таким образом возникает зона проводимости, в которой электроны могут изменять свое состояние под внешним воздействием, занимая выше лежащие свободные энергетические уровни. Если, например, приложено электрическое поле, то электроны приобретут дополнительную скорость вдоль поля и, соответственно, энергию, будет осуществляться перенос электрического заряда, т.е. течь электрический ток.

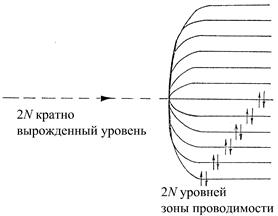
Рис. 1.2

Электроны являются фермионами с полуцелым спином и описываются статистикой ФермиДирака, согласно которой плотность частиц в фазовом пространстве (пространстве импульсов и координат) или функция распределения f имеет вид [ ]

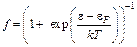, (1.3)

где _F  энергия Ферми, k  константа Больцмана, Т  температура электронов в градусах Кельвина. Суммируя фазовую плотность частиц по всем возможным значениям импульса (связь f с импульсом определяется посредством зависимости энергии от импульса согласно формуле (1.1)), находим концентрацию частиц n (количество частиц в единице объема)

. (1.4)

Двойка в формуле (1.4) появилась за счет двух возможных значений проекции спина. В квантовой статистике есть правило перехода от суммирования по импульсам к интегрированию.

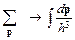, (1.5),

h  постоянная Планка или в, данном случае, объем элементарной ячейки в фазовом пространстве в соответствии с соотношением неопределенности. Используя (1.5) в (1.4) и переходя к сферической системе координат в пространстве импульсов (см. рис. 1.3 и приведенные ниже преобразования),

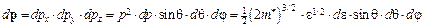, (1.6)

получаем

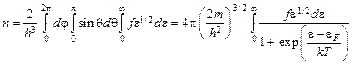. (1.7)

Формула (1.7) дает связь между концентрацией электронов проводимости n и энергией Ферми _F. В общем случае интеграл в (1.7) в элементарных функциях не выражается. Поэтому используют два основных приближения.

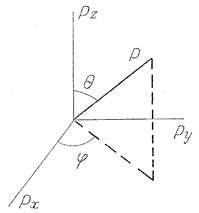
Рис. 1.3

1) Вырожденный электронный газ

В этом случае температура электронов мала. Количественно этот критерий записывается в виде

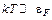(1.8)

При вычислениях используют особенности зависимости функции распределения ее производной от энергии (см. рис. 1.4). Как видно из рис. 1.4, функция f близка по форме к ступеньке (  функция Хевисайда), а ее производная  к -функции Дирака. Учитывая это обстоятельство, из (1.7) получают

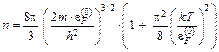(1.9)

или

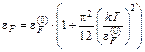, (1.10)

где

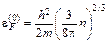. (1.11)

В “хороших” металлах n » 10²³ cм^3и 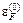» 5 эВ. Напомним, что один электрон-вольт 1 эВ = 1.6 ´ 10^12эрг. Учитывая (1.11), критерий вырождения (1.8) можно переписать в виде

.

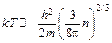(1.12)

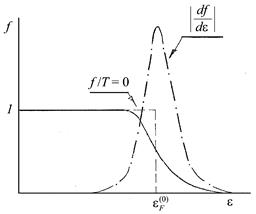
Рис. 1.4

2) Невырожденный электронный газ

В этом случае уровень Ферми отрицателен и функцию распределения можно представить в виде

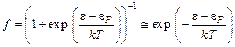. (1.13)

Подстановка (1.7) в (1.13) дает

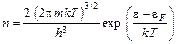(1.14)

и

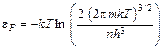. (1.15)

Критерий невырожденности можно записать как

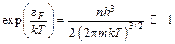. (1.16)

Сравнивая критерии (1.12) и (1.16), мы видим, что высокая концентрация приводит к вырождению электронов проводимости, в то время как требование невырожденности (классичности) ограничивает концентрацию сверху. В металлах с хорошей электропроводностью и высокой эмиссионной способностью реализуется первый случай.