Объемная плотность энергии
Энергию заряженных проводников и конденсаторов обычно определяют через их заряды и потенциалы. Можно, однако, связать энергию заряженной системы с характеристиками ее электрического поля. Для этого рассмотрим плоский конденсатор, параметры которого указаны на рисунке 52.1.
Воспользуемся формулой (51.5) и выполним преобразования с учетом выражений (41.2) и (35.3):
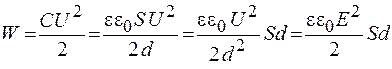 . (52.1)
. (52.1)
Величина 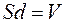 - объем пространства между пластинами конденсатора. Пренебрегая искажениями поля у краев пластин (краевым эффектом), можно считать, что поле конденсатора сосредоточено между его обкладками. Тогда V - это и объем электрического поля. В соответствии с этим формулу (52.1) запишем в виде
- объем пространства между пластинами конденсатора. Пренебрегая искажениями поля у краев пластин (краевым эффектом), можно считать, что поле конденсатора сосредоточено между его обкладками. Тогда V - это и объем электрического поля. В соответствии с этим формулу (52.1) запишем в виде
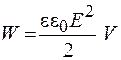 . (52.2)
. (52.2)
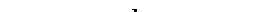 Выражение (52.2) определяет энергию заряженного конденсатора через характеристики электрического поля: его напряженность Е и объем V. На основе этого можно сделать вывод о том, что энергия локализована в электрическом поле, что само поле обладает энергией, а не электрический заряд. По этому поводу следует сказать, что в электростатике нет ответа на данный вопрос, так как рассматриваются стационарные поля, создаваемые электрическими зарядами. Переменные поля могут существовать независимо от электрических зарядов и распространяться в виде электромагнитных волн. Перенос энергии электромагнитными волнами доказан экспериментально и применяется в телекоммуникационных системах. Это дает основание утверждать, что электрическое поле является носителем энергии. Следовательно, этим уравнением определяется энергия электрического поля. Связь энергии поля с его объемом подтверждает материальность электрического поля.
Выражение (52.2) определяет энергию заряженного конденсатора через характеристики электрического поля: его напряженность Е и объем V. На основе этого можно сделать вывод о том, что энергия локализована в электрическом поле, что само поле обладает энергией, а не электрический заряд. По этому поводу следует сказать, что в электростатике нет ответа на данный вопрос, так как рассматриваются стационарные поля, создаваемые электрическими зарядами. Переменные поля могут существовать независимо от электрических зарядов и распространяться в виде электромагнитных волн. Перенос энергии электромагнитными волнами доказан экспериментально и применяется в телекоммуникационных системах. Это дает основание утверждать, что электрическое поле является носителем энергии. Следовательно, этим уравнением определяется энергия электрического поля. Связь энергии поля с его объемом подтверждает материальность электрического поля.
Значение энергии, приходящейся на единицу объема поля, называется объемной плотностью энергии 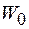 .
.
Поле плоского конденсатора однородно и энергия распределена в нем с одинаковой плотностью. Поэтому можно записать:
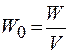 . (52.3)
. (52.3)
Единица объемной плотности энергии - джоуль на метр в кубе 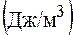 . Объединив формулы (52.3) и (52.2), получаем
. Объединив формулы (52.3) и (52.2), получаем
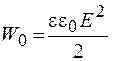 .
.
Выполним преобразования с использованием выражения (47.1):
 . (52.4)
. (52.4)
Воспользуемся уравнением 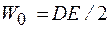 и заменим в нем электрическое смещение D в соответствии с формулой (47.6):
и заменим в нем электрическое смещение D в соответствии с формулой (47.6):
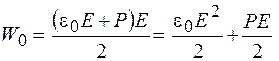 . (52.5)
. (52.5)
Первое слагаемое в этом выражении совпадает с плотностью энергии электрического поля в вакууме ( 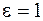 ), второе слагаемое представляет собой энергию, затраченную на поляризацию диэлектрика.
), второе слагаемое представляет собой энергию, затраченную на поляризацию диэлектрика.
Формулы для плотности энергии были получены для однородного поля, но они применимы для всякого поля в изотропном диэлектрике. Это позволяет рассчитать энергию поля, заключенную в любом объеме:
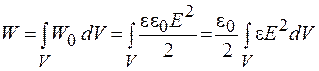 , (52.6)
, (52.6)
где для неоднородного поля напряженность должна быть задана функцией 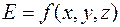 .
.
Дата добавления: 2015-08-08; просмотров: 2893;
