Конденсатора

Рассмотрим проводник, которому сообщен заряд q. В состоянии равновесия потенциалы всех точек проводника одинаковы и равны j. Заряд проводника можно представить в виде системы точечных зарядов 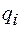. Тогда для энергии проводника можно воспользоваться выражением (50.3), записав его в виде

,

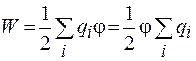где 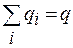- полный заряд проводника.

Тогда получаем

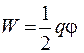. (51.1)

Если воспользоваться соотношением 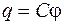, то из формулы (51.1) можно получить

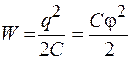. (51.2)

Полученные формулы являются равноценными и, подчеркивая этот факт, запишем их в одной строке:

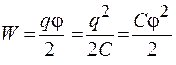. (51.3)

Рассчитаем теперь энергию заряженного конденсатора. При зарядке на его обкладках накапливаются равные по модулю, но противоположные по знаку заряды. Процесс зарядки можно представить как перенос малых порций заряда dq с одной обкладки на другую (рис. 51.1).

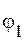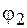Вследствие малости величины dq можно утверждать, что ее перенос практически не изменит потенциалов и обкладок. При перемещении одной порции заряда dq против сил поля внешними силами совершается элементарная работа

.

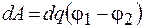Выразив разность потенциалов из формулы (41.1) 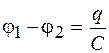, элементарную работу представим в виде

.

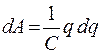Полная работа зарядки конденсатора соответствует изменению заряда от 0 до q. Поэтому

.

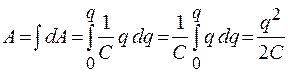Работа внешних сил равна сообщенной конденсатору энергии, т. е. А = W. Следовательно,

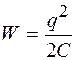. (51.4)

С учетом соотношения (41.1) формулу (51.4) можно преобразовать к виду

,

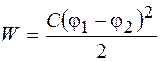или

.

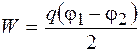Как отмечалось ранее, разность потенциалов на обкладках конденсатора иначе называется напряжением: 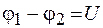. В соответствии с этим полученные выражения преобразуем к виду

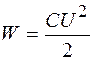, (51.5)

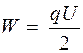. (51.6)

Запишем формулы энергии заряженного конденсатора (5.4–5.6) в одной строке:

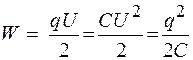. (51.7)

Энергия заряженного конденсатора тем больше, чем больше заряд и напряжение на его обкладках.

Сравнивая выражения (51.7) и (51.3), следует отметить их одинаковый вид.