Закон Ома в интегральной и дифференциальной

Формах

Г. С. Ом в 1826 г. установил, что сила тока на однородном участке цепи прямо пропорциональна напряжению U (разности потенциалов) на концах проводника:

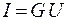, (54.1)

где G - электрическая проводимость. Она зависит от материала, формы и размеров проводника, его температуры.

Величина, обратная электрической проводимости

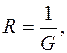
называется электрическим сопротивлением (для краткости - сопротивлением) проводника.

Сопротивление также зависит от температуры, формы, размеров проводника и свойств материала, из которого он изготовлен. Для однородного цилиндрического проводника длиной l и площадью поперечного сечения S сопротивление определяется формулой

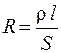. (54.2)

Входящая в нее величина r называется удельным сопротивлением итакже зависит от материала и температуры. У металлов при нагревании удельное сопротивление увеличивается по линейному закону:

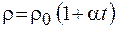r, (54.3)

где 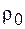- удельное сопротивление при 0 °C, 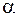- температурный коэффициент сопротивления, t - температура по шкале Цельсия.

Объединяя формулы (54.1) и (54.2) находим

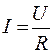. (54.4)

Выражения (54.1) и (54.4) называют законом Ома для однородного участка цепи, или законом Ома в интегральной форме.

Подставим выражение (54.2) в уравнение (54.4) и выполним преобразования:

,

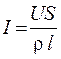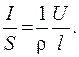(54.5)

Производим замену:

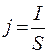- плотность тока,

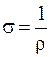- удельная проводимость вещества,

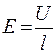– напряженность электрического поля в проводнике.

В итоге уравнение (54.5) приводим к виду

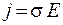. (54.6)

Формула (54.6) описывает закон Ома в дифференциальной форме: плотность тока прямо пропорциональна напряженности электрического поля в проводнике.

В каждой точке проводника 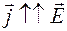, поэтому выражение (54.6) можем записать в векторной форме:

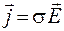. (54.7)

Единица электрической проводимости - сименс (См), единица сопротивления - ом (1 Ом =1 См^-1), удельного сопротивления - ом-метр ( 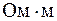). Поскольку удельная проводимость 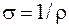, то ее единица - сименс на метр (См/м).