Разветвленные цепи. Правила Кирхгофа

При описании сложных разветвленных электрических цепей будем использовать понятия:

узел - точка, в которой сходится более чем два проводника;

ветвь - участок между двумя узлами, в пределах которого течет один и тот же ток;

контур - замкнутый контур из нескольких последовательных участков.

Расчеты таких цепей значительно упрощаются с применением правил, сформулированных Г. Кирхгофом.

Первое правило Кирхгофа: алгебраическая сумма сил токов в узле равна нулю:

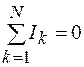. (57.1)

Выражение (57.1) является следствием закона сохранения заряда.

Ток, направленный к узлу, принимается положительным, направленный от узла, - отрицательным. Для узла А на рисунке 57.1 по первому правилу Кирхгофа 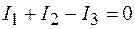. Если контур содержит N узлов, то по первому правилу Кирхгофа записывают (N - 1) уравнений, так как N-е уравнение будет следствием из них.

Рассмотрим замкнутый контур АВСА, выделенный в разветвленной цепи (рис. 57.2). Он включает в себя три узла с потенциалами 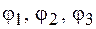и три ветви с силами токов 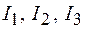, сопротивлениями 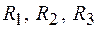и электродвижущими силами 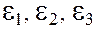соответственно.

Зададим произвольно направление обхода контура (например, против часовой стрелки, как указано на рисунке 57.2), применим к каждой ветви контура закон Ома для неоднородного участка цепи:

;

;

.

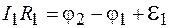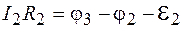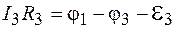Находим сумму падений напряжения:

.

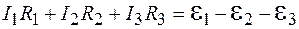В общем виде это уравнение принимает вид

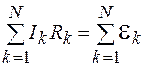, (57.2)

где N – число ветвей в контуре.

Уравнение (57.2) представляет собой второе правило Кирхгофа, согласно которому алгебраическая сумма падений напряжения на участках замкнутого контура равна алгебраической сумме ЭДС источников, включенных в этот контур.

Второе правило Кирхгофа можно применить для всех контуров электрической цепи. Однако независимыми будут уравнения для тех контуров, которые нельзя получить наложением друг на друга ранее рассмотренных контуров.

При составлении уравнений на основании второго правила Кирхгофа токам и ЭДС нужно приписывать знаки в соответствии с выбранным направлением обхода. Если направление тока в участке совпадает с направлением обхода контура, то произведение 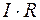для этого участка берется со знаком "плюс" и наоборот. Если в направлении обхода источник тока повышает потенциал (переход через источник от "минуса" к "плюсу"), то ЭДС такого источника входит в уравнение со знаком "плюс" и наоборот.

В связи с этим правилом знаков может возникнуть кажущееся затруднение при составлении уравнений. Ведь направления отдельных токов заранее не известны и должны быть найдены из решения задачи, тогда как само составление уравнений требует знания этих направлений. Однако на самом деле этой трудности не существует. При составлении уравнений можно с самого начала произвольно выбрать для каждой ветви некоторые направления токов. Единственное, что при этом необходимо учитывать, это то, чтобы все токи не входили в любой узел или не выходили из него. Реальное направление токов определится решением задачи: если сила тока окажется положительной, то его направление совпадает с предполагаемым, если отрицательной, то, значит, в действительности ток направлен противоположно выбранному направлению.

Рассмотренные закономерности позволяют предложить план решения задач с применение правил Кирхгофа:

1. Указать предположительно направление токов в ветвях.

2. Выбрать направление обхода контуров.

3. Составить уравнения для токов в узлах и суммы напряжений в контурах так, чтобы их число соответствовало числу неизвестных величин.

4. Решить систему уравнений.