Два целых числа и называются сравнимыми по модулю , если при делении на это число они дают одинаковые остатки. 4 страница

, .

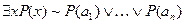Заменяя все кванторы по этим соотношениям, любую формулу логики предикатов можно перевести в формулу, состоящую из предикатов, соединённых логическими операциями. Истинность такой формулы на конечной области проверятся конечным числом подстановок и вычислений. Методы рассуждений, использующие только конечные множества конечных объектов, называются финитными.

Для бесконечных же областей, в общем случае, при доказательстве тождественной истинности формул метод интерпретации связан с большими трудностями. Поэтому для построения множества истинных формул в логике предикатов выбирается иной путь. Это множество порождается из неких исходных формул (аксиом) с помощью формальных процедур - правил вывода. Используются лишь формальные (а не содержательные), внешние свойства последовательности символов, образующих формулы, причём эти свойства полностью описываются правилами вывода. Множества, порождённые таким формальным методом, называются формальными.

Лекция № 13. Комбинаторика.

В этой лекции даются основные начальные сведения из комбинаторики. Это служебный раздел математики, занимающийся исследованием различных комбинаций элементов всевозможных множеств. Формулы комбинаторики широко используются теории вероятностей, в теории вычислительных машин, в некоторых разделах экономике, в статистике и других прикладных дисциплинах.

1. Правила суммы и произведения.

Будем в дальнейшем оперировать только с множествами, содержащими конечное число элементов. На бесконечные множества все нижеприведённые правила и формулы не распространяются.

Теорема 13.1. Пусть даны непересекающиеся конечные множества 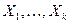. Тогда мощность объединения этих множеств равна сумме мощностей данных множеств:

.

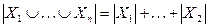Доказательство этой теоремы очевидно. Но для нас представляет интерес другая интерпретация этой теоремы, которую мы сформулируем для двух множеств.

Если некоторый элемент 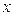можно выбрать 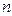способами, а элемент 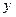- 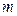способами, причём любой способ выбора элемента 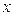отличается от любого способа выбора элемента 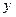, то выбор “ 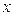или 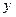” можно сделать 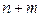способами. Это правило называется правилом суммы.

Пусть даны непересекающиеся конечные множества 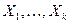. Обозначим число элементов в этих множествах (их мощности) 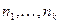. Рассмотрим декартово произведение этих множеств 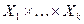. Напомним, что элементами этого произведения будут векторы (кортежи) длины 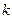вида .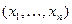

Теорема 13.2. Число элементов в декартовом произведении множеств 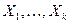равно произведению мощностей этих множеств:

.

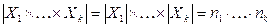Как и в предыдущем случае, сформулируем данную теорему упрощённым образом для двух множеств. Если элемент 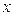можно выбрать 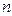способами, а элемент 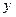- 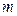способами, причём любой способ выбора элемента 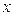отличается от любого способа выбора элемента 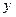, то выбор “ 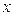и 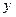” (то есть, пары 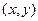) можно сделать 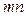способами. Это правило называется правилом произведения, или умножения.

Оба сформулированных правила верны для любого конечного числа конечных множеств, и, в соответствующей форме, называются обобщёнными.

Пример 1.

а) В некоторой средней школе имеется три пятых класса, в которых обучаются соответственно 28, 31 и 26 учащихся. Требуется одного из них выбрать для участия в совете школы. Сколькими способами можно сделать выбор?

По правилу суммы получаем .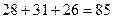

б) В секции фигурного катания занимаются 14 мальчиков и 18 девочек. Сколькими различными способами из детей, занимающихся в секции, можно образовать спортивные пары.

По правилу произведения получаем .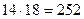

1. Размещения.

Определение. Любой вектор длины 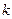, составленный из элементов 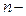элементного множества 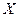, в котором все элементы различны, называется размещением без повторений по 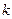элементов из 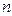. Число всех размещений без повторений по 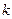элементов из 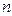обозначается 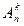и равно .

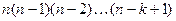Пример 2. Куплено различных 12 книг. На полке можно поставить в ряд ровно 6 книг. Сколькими различными способами можно это сделать?

Будем считать различными не только те случаи, когда берутся разные книги, но и когда они по-разному расставлены на полке (в различном порядке). Тогда речь идёт о перестановках по 6 из 12. Получаем: .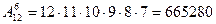

Рассмотрим существенно другой случай, а именно когда элементы множества 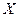в векторах могут повторяться.

Определение. Любой вектор длины 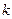, составленный из элементов 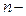элементного множества 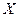, состоящего из 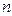элементов, в котором все элементы различны, называется размещением с повторениями по 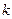элементов из 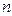. Число всех размещений с повторениями по 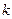элементов из 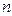обозначается 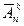и равно .

Пример 3. Сколько различных комбинаций может получиться при одновременном бросании трёх игральных костей?

Каждая игральная кость представляет собой кубик, на гранях которого нанесено от одного до 6 очков. При каждом бросании мы будем получать наборы вида 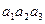, где 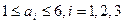- количество очков, выпавших на соответствующей кости. Речь идёт о перестановках с повторениями по 3 элемента из 6. Получаем: .

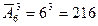Замечание. Очевидно, что размещения без повторений являются частным случаем размещений с повторениями.

1. Перестановки.

Определение. Любой вектор длины 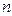, составленный из элементов 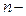элементного множества 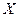, в котором все элементы различны, называется перестановкой без повторений из 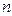элементов. Число всех перестановок без повторений из 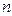элементов обозначается 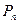и равно .

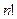Из определения и формулы видно, что перестановки без повторений есть частный случай размещений без повторений, при условии .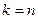

Пример 4. Сколькими различными способами можно расставить на полке 10 различных книг?

Здесь, в отличие от примера 2, значение имеет только порядок расставляемых книг. Поэтому речь идёт о перестановках из 10 элементов. Получаем: .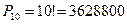

Рассмотрим случай, когда элементы множества 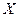повторяются по нескольку раз. Для определённости пусть 1-й элемент повторяется 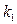раз, 2-й элемент - 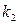раз и так далее. Тогда векторы длины 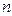, образованные из элементов данного множества называются перестановками из 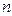элементов с повторениями. Число таких перестановок обозначается 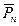и равно .

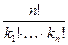Положив в последней формуле 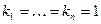, получим формулу для перестановок без повторений.

Пример 5. Сколько различных шестизначных чисел могут быть записано с помощью цифр 1, 2, 2, 2, 3, 3?

Имеется набор из шести цифр, в котором цифра 2 повторяется трижды и цифра 3 – дважды. Полученные числа будут представлять собой перестановки с повторениями из 6 элементов. Получаем: .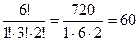

1. Сочетания. Бином Ньютона.

Прежде всего, отметим одно существенное отличие перестановок от размещений. Если в размещениях векторы различаются и по составу элементов, и по их расположению (порядку) в наборе, то в перестановках векторы различаются только по расположению элементов. Естественно рассмотреть случай, когда векторы, наоборот, будут различаться только по составу элементов.

Определение. Любые различные векторы длины 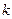, составленные из элементов 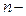элементного множества 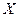, различающиеся между собой по набору элементов, но не по их расположению в наборе, называются сочетаниями по 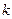элементов из .

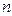Если все элементы, образующие сочетания, различны, то их называют сочетанием без повторений. Обозначение всех сочетаний без повторений 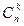. Формула для вычисления 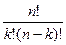. Если некоторые (или все) элементы, образующие сочетания, могут повторяться, то их называют сочетаниями повторениями. Обозначение всех сочетаний без повторений 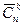. Формула для вычисления 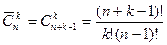. Запоминать последнюю формулу нет необходимости.

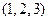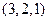Замечание 1. Сочетания являются частным случаем размещений. Разница между сочетаниями и размещениями из определения неочевидна, но на конкретных примерах её легко видеть. Так, например, векторы и являются различными размещениями, но обозначают одно и то же сочетание.

Замечание 2. Для сочетаний без повторений обязательно требование 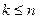, причём в случае равенства получим естественный результат 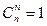. Но для сочетаний с повторениями это требование необязательно, как будет видно из приведённого ниже примера.

Пример 6.

а) В отделе работают 10 сотрудников. Требуется отобрать трёх из них для того, чтобы направить в командировку. Сколькими способами можно это сделать?

Поскольку имеет значение только то, какие именно сотрудники отобраны, то речь идёт о сочетаниях без повторений по 3 элемента из 10. Получаем: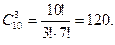

б) В цветочном магазине имеются в продаже 5 различных видов цветов. Покупателю требуется составить букет из 7 цветов. Сколькими способами можно это сделать?

Будем считать различными те букеты, которые отличаются друг от друга по подбору цветов. Поскольку цветы в букете могут повторяться, то речь идёт о сочетаниях с повторениями по 7 элементов из 5. Тогда получим .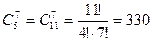

Одним из наиболее известных примеров использования комбинаторных формул является так называемый бином Ньютона. В общем виде формула бинома (двучлена) Ньютона выглядит так:

.

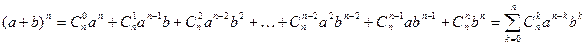С частными случаями применения этой формулы ( для случаев 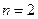и 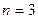) сталкиваются ещё в школе при изучении формул сокращённого умножения:

.

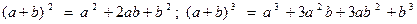На практике для удобства применении бинома Ньютона применяют так называемый треугольник Паскаля, который содержит числовые коэффициенты полинома в правой части формулы:

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

…………………..