Два целых числа и называются сравнимыми по модулю , если при делении на это число они дают одинаковые остатки. 2 страница
Пример 1. Если рассматривать логические функции, то, очевидно, дизъюнкция двойственна конъюнкции и наоборот (непосредственно следует из правил Де Моргана). Отрицание является самодвойственной функцией. Функция-константа 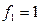 двойственна функции
двойственна функции 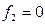 . Ещё один традиционный пример самодвойственной функции – функция
. Ещё один традиционный пример самодвойственной функции – функция 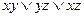 .
.
Пользуясь определением двойственности нетрудно доказать следующее утверждение, называемое принципом двойственности.
Теорема 10.1. Если в формуле 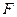 , представляющей функцию
, представляющей функцию 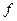 , все знаки функций заменить соответственно на знаки двойственных им функций, то полученная формула
, все знаки функций заменить соответственно на знаки двойственных им функций, то полученная формула 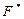 будет представлять функцию
будет представлять функцию 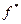 , двойственную функции
, двойственную функции 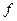 .
.
В булевой алгебре принцип двойственности имеет более конкретный вид, вытекающий из ранее приведённых примеров: если в формуле 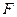 , представляющей функцию
, представляющей функцию 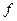 , все конъюнкции заменить дизъюнкциями и наоборот, все единицы заменить нулями и наоборот, то получим формулу
, все конъюнкции заменить дизъюнкциями и наоборот, все единицы заменить нулями и наоборот, то получим формулу 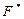 , представляющую функцию
, представляющую функцию 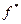 , двойственную функции
, двойственную функции 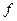 .
.
Если функции равны, то двойственные им функции также равны. Это позволяет с помощью принципа двойственности получать новые эквивалентные соотношения, переходя от равенства 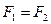 с помощью указанных замен к равенству
с помощью указанных замен к равенству 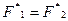 . Примером могут служить соотношения
. Примером могут служить соотношения 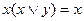 и
и 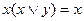 , которые могут быть получены друг из друга по указанному принципу.
, которые могут быть получены друг из друга по указанному принципу.
- Булева алгебра и теория множеств.
Ранее были описаны булевы алгебры множеств, то есть алгебры вида 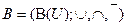 , где
, где 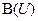 - булеан множества
- булеан множества 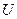 , то есть множество всех его подмножеств. Общий термин “булева алгебра” для алгебр множеств и логических функций не является случайным.
, то есть множество всех его подмножеств. Общий термин “булева алгебра” для алгебр множеств и логических функций не является случайным.
Определение. Всякая алгебра типа 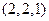 называется булевой алгеброй, если её операции удовлетворяют соотношениям 1 – 10 (см. предыдущую лекцию).
называется булевой алгеброй, если её операции удовлетворяют соотношениям 1 – 10 (см. предыдущую лекцию).
В алгебре множеств элементами являются подмножества фиксированного универсального множества 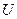 . В этой алгебре операция пересечения соответствует конъюнкции, операция объединения соответствует дизъюнкции, а операция дополнения соответствует отрицанию. Само множество
. В этой алгебре операция пересечения соответствует конъюнкции, операция объединения соответствует дизъюнкции, а операция дополнения соответствует отрицанию. Само множество 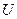 является единицей, а пустое множество – нулём. Справедливость соотношений 1 – 10 для этой алгебры можно доказать непосредственно, рассматривая в них переменные как множества, а знаки логических функций – как соответствующие операции над множествами.
является единицей, а пустое множество – нулём. Справедливость соотношений 1 – 10 для этой алгебры можно доказать непосредственно, рассматривая в них переменные как множества, а знаки логических функций – как соответствующие операции над множествами.
В одной из предыдущих лекций отмечалось взаимно однозначное соответствие между множеством 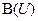 , где
, где 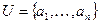 и множеством
и множеством 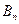 двоичных векторов длины
двоичных векторов длины 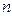 . Каждому подмножеству
. Каждому подмножеству 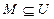 соответствует двоичный вектор
соответствует двоичный вектор 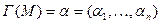 , где
, где 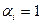 , если
, если 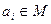 , и
, и 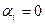 , если
, если 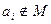 . Операции над векторами в булевой алгебре
. Операции над векторами в булевой алгебре 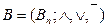 определяются следующим образом.
определяются следующим образом.
Пусть даны два вектора 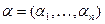 и
и 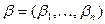 из множества
из множества 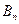 . Тогда:
. Тогда:
 ,
,
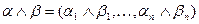 ,
,
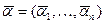 .
.
Поскольку компоненты (координаты) векторов принимают значения 0 или 1, то указанные операции – это просто логические операции над двоичными переменными, поэтому операции над векторами естественно назвать покомпонентными логическими операциями над двоичными векторами.
Пример 2. Даны векторы 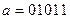 и
и 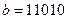 . Найти
. Найти 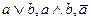 .
.
Решение:
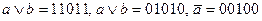 .
.
Заметим, что подобные операции (наряду с логическими операциями над переменными) входят в систему команд любой современной ЭВМ.
Теорема 10.2. Если мощность множества 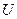 равна
равна 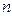
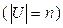 , то булева алгебра
, то булева алгебра 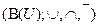 изоморфна булевой алгебре
изоморфна булевой алгебре  .
.
Эта простая по содержанию теорема имеет огромное значение в математике. Она позволяет заменить теоретико-множественные операции над системой подмножеств данного множества поразрядными логическими операциями над двоичными векторами.
Похожая по формулировке, но значительно отличающаяся по смыслу теорема существует для множества всех логических функций 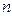 переменных
переменных 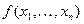 . Обозначим это множество
. Обозначим это множество 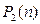 . Оно замкнуто относительно операций
. Оно замкнуто относительно операций 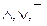 и, следовательно, образует конечную булеву алгебру
и, следовательно, образует конечную булеву алгебру 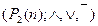 , которая является подалгеброй булевой алгебры логических функций.
, которая является подалгеброй булевой алгебры логических функций.
Теорема 10.3. Если мощность множества 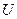 равна
равна 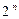
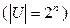 , то булева алгебра
, то булева алгебра 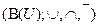 изоморфна булевой алгебре функций
изоморфна булевой алгебре функций 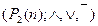 .
.
Теорема 10.3 указывает на тесную связь между множествами и логическими функциями и позволяет переходить от операций над множествами к операциям над функциями и обратно. В частности, они позволяют непосредственно производить операции над функциями, заданными не формулами, а таблицами. Пример приведён в следующей таблице, содержащей две функции трёх переменных 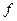 и
и 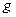 и результаты операций над ними:
и результаты операций над ними:
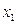
| 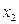
| 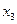
| 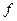
| 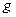
| 
| 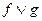
| 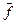
|
- ДНФ, интервалы и покрытия.
Теоретико-множественная интерпретация булевой алгебры предлагает очень удобный язык для изучения дизъюнктивных нормальных форм (ДНФ) и построения методов их упрощения. Рассмотрим кратко основные понятия, связанные с ДНФ.
Введём следующее обозначение: обозначим через 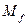 множество всех единичных наборов функции
множество всех единичных наборов функции 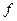 . Тогда набор (вектор)
. Тогда набор (вектор) 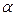 из множества
из множества 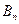 принадлежит
принадлежит 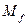 тогда и только тогда, когда
тогда и только тогда, когда 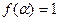 . Множество
. Множество 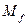 называется единичным множеством функции
называется единичным множеством функции 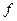 , а функция
, а функция 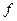 называется характеристической функцией множества
называется характеристической функцией множества 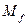 . Легко показать, что соответствие между функциями и их единичными множествами является изоморфизмом.
. Легко показать, что соответствие между функциями и их единичными множествами является изоморфизмом.
Если функция 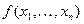 представляется элементарной конъюнкцией всех
представляется элементарной конъюнкцией всех 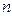 переменных, то множество
переменных, то множество 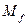 содержит ровно один элемент множества
содержит ровно один элемент множества 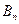 . Если же функция – элементарная конъюнкция
. Если же функция – элементарная конъюнкция 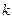 переменных
переменных 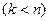 , то
, то 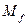 содержит
содержит 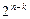 двоичных наборов. Это объясняется тем, что в таком случае
двоичных наборов. Это объясняется тем, что в таком случае 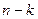 переменных, не входящих в эту конъюнкцию несущественны для функции
переменных, не входящих в эту конъюнкцию несущественны для функции 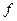 . Тогда они принимают
. Тогда они принимают 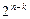 значений, не изменяя значения
значений, не изменяя значения 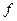 . Множество
. Множество 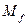 такой функции называется интервалом.
такой функции называется интервалом.
Пример 3. Рассмотрим функцию  и найдём её интервал.
и найдём её интервал.
Прежде всего, заметим, что две переменных 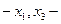 являются несущественными. Это позволяет сразу определить количество единичных наборов, содержащихся в множестве
являются несущественными. Это позволяет сразу определить количество единичных наборов, содержащихся в множестве 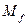 (иначе говоря, его мощность). Поскольку в данном случае
(иначе говоря, его мощность). Поскольку в данном случае 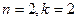 , то получим
, то получим 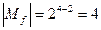 .
.
Далее, очевидно, что 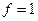 только при значениях
только при значениях  . При этом переменные
. При этом переменные 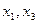 могут принимать любые значения. Теперь перечислим все единичные наборы для данной функции:
могут принимать любые значения. Теперь перечислим все единичные наборы для данной функции: 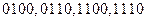 . Итак,
. Итак, 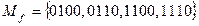 .
.
В рассматриваемом случае говорят, что конъюнкция 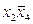 (или, точнее, интервал
(или, точнее, интервал 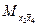 ) покрывает множество
) покрывает множество 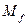 и все его подмножества.
и все его подмножества.
Представление некоторой функции в виде ДНФ соответствует представлению её единичного множества в виде объединения интервалов; в совокупности все конъюнкции ДНФ покрывают всё единичное множество функции 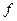 . Обратное также верно: если все элементы некоторого интервала
. Обратное также верно: если все элементы некоторого интервала 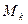 принадлежат
принадлежат 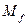 , то существует ДНФ данной функции, содержащая конъюнкцию
, то существует ДНФ данной функции, содержащая конъюнкцию 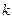 .
.
Лекция № 11. Полнота и замкнутость.
Ранее нами рассматривались два способа задания логических функций – табличный и с помощью формул. Таблица задаёт функцию непосредственно как соответствие между двоичными наборами и значениями функции на этих наборах. Этот способ универсален, то есть, пригоден для любых функций, однако слишком громоздок. Формула – гораздо более компактный способ задания функции, но она задаёт функцию через другие функции. Поэтому для любой системы функций 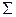 возникает естественный вопрос: всякая ли логическая функция представима формулой в этой системе. В позапрошлой лекции был получен положительный ответ для системы
возникает естественный вопрос: всякая ли логическая функция представима формулой в этой системе. В позапрошлой лекции был получен положительный ответ для системы 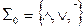 (теорема 8.2). В данной лекции будет показано, как решать этот вопрос для произвольной системы
(теорема 8.2). В данной лекции будет показано, как решать этот вопрос для произвольной системы 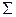 .
.
- Функционально полные системы.
Определение. Система функций 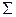 называется функционально полной системой, если любая логическая функция может быть представлена формулой над системой
называется функционально полной системой, если любая логическая функция может быть представлена формулой над системой 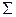 (является суперпозицией функций этой системы).
(является суперпозицией функций этой системы).
Из теоремы 8.2 следует, что система 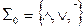 является функционально полной. Равным образом, функционально полна любая система
является функционально полной. Равным образом, функционально полна любая система 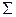 , через функции которой можно выразить конъюнкцию, дизъюнкцию и отрицание. Действительно, для любой логической функции
, через функции которой можно выразить конъюнкцию, дизъюнкцию и отрицание. Действительно, для любой логической функции 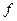 из такой системы следует составить булеву формулу (а она обязательно существует согласно теореме 8.2) и потом выразить в ней конъюнкцию, дизъюнкцию и отрицание через функции системы
из такой системы следует составить булеву формулу (а она обязательно существует согласно теореме 8.2) и потом выразить в ней конъюнкцию, дизъюнкцию и отрицание через функции системы 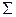 . Аналогично обосновывается более общее утверждение.
. Аналогично обосновывается более общее утверждение.
Теорема 11.1. Если все функции функционально полной системы 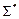 представимы формулами над системой
представимы формулами над системой 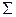 , то система
, то система 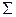 также функционально полна.
также функционально полна.
Пример 1.
а) Системы 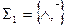 и
и 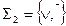 функционально полны. Действительно, с помощью законов Де Моргана и двойного отрицания можно выразить в каждой из этих систем функцию, недостающую до
функционально полны. Действительно, с помощью законов Де Моргана и двойного отрицания можно выразить в каждой из этих систем функцию, недостающую до 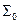 через остальные две:
через остальные две:
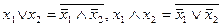 .
.
С точки зрения функциональной полноты систему 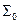 следует считать избыточной: она сохраняет свойство полноты и при удалении из неё конъюнкции или дизъюнкции. Однако легко видеть из приведённого примера, что, хотя системы
следует считать избыточной: она сохраняет свойство полноты и при удалении из неё конъюнкции или дизъюнкции. Однако легко видеть из приведённого примера, что, хотя системы 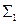 и
и 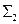 не являются избыточными, зато формулы в них получаются гораздо длиннее: замена одной операции на другую вносит в формулу сразу три лишних отрицания.
не являются избыточными, зато формулы в них получаются гораздо длиннее: замена одной операции на другую вносит в формулу сразу три лишних отрицания.
б) Системы 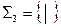 (штрих Шеффера) и
(штрих Шеффера) и 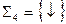 (стрелка Пирса) являются функционально полными.
(стрелка Пирса) являются функционально полными.
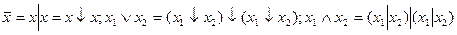 .
.
Таким образом, система 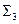 сводится к системе
сводится к системе 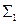 , а система
, а система 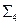 - к системе
- к системе 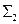 .
.
в) Система 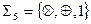 (
( 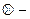 умножение по модулю 2,
умножение по модулю 2, 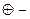 сложение по модулю 2 – см. пункт 1 лекции № 8)) является функционально полной. Поскольку
сложение по модулю 2 – см. пункт 1 лекции № 8)) является функционально полной. Поскольку 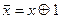 , данная система сводится к
, данная система сводится к 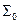 .
.
На свойствах этой системы остановимся подробнее.
- Алгебра Жегалкина и линейные функции.
Определение. Алгебра над множеством логических функций с двумя бинарными операциями 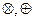 называется алгеброй Жегалкина.
называется алгеброй Жегалкина.
Замечание. Операция 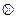 вполне аналогична операции конъюнкции (логического умножения). Однако операция
вполне аналогична операции конъюнкции (логического умножения). Однако операция 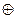 имеет совершенно другой математический смысл, чем дизъюнкция (соответствующая функция ранее была названа неравнозначностью). Поэтому никак нельзя считать алгебру Жегалкина иной формой записи булевой алгебры.
имеет совершенно другой математический смысл, чем дизъюнкция (соответствующая функция ранее была названа неравнозначностью). Поэтому никак нельзя считать алгебру Жегалкина иной формой записи булевой алгебры.
В алгебре Жегалкина выполняются следующие соотношения (знак умножения 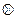 опущен):
опущен):
2.1. 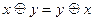 ,
,
2.2. 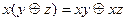 ,
,
2.3 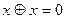 ,
,
2.4 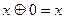 .
.
Кроме того, выполняются соотношения, ранее сформулированные булевой алгебры, относящиеся к конъюнкции и константам. Отрицание и дизъюнкция выражаются так:
2.5 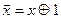 ,
,
2.6  .
.
Если в произвольной формуле алгебры Жегалкина раскрыть скобки и произвести все упрощения по вышеуказанным соотношениям, то получится формула, имеющая вид Суммы произведений, то есть полином (многочлен) по модулю 2. Такая формула называется полиномом Жегалкина для данной функции.
От булевой формулы всегда можно перейти к формуле алгебры Жегалкина, используя равенства 2.5 и 2.6, а также прямое следствие из равенства 2.6: если 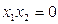 , то
, то 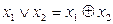 . Оно, в частности, позволяет заменять знак дизъюнкции знаком
. Оно, в частности, позволяет заменять знак дизъюнкции знаком 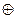 в случаях, когда исходная формула представляет собой СДНФ.
в случаях, когда исходная формула представляет собой СДНФ.
Пример 2. Составить полиномы Жегалкина для данных функций:
а)  ,
,
б) 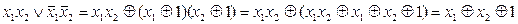 .
.
Заметим, что если в полученных полиномах Жегалкина произвести обратную замену функций, то получим упрощённые формулы булевой алгебры.
Теорема 11.2. Для всякой логической функции существует полином Жегалкина и притом единственный.
Существование такого полинома, по сути, уже доказано, а для доказательства его единственности достаточно показать существование взаимно однозначного соответствия между множеством всех функций 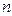 переменных и множеством всех полиномов Жегалкина.
переменных и множеством всех полиномов Жегалкина.
Определение. Функция, у которой полином Жегалкина имеет вид 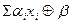 , где параметры
, где параметры 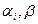 равны нулю или единице, называется линейной.
равны нулю или единице, называется линейной.
Все функции от одной переменной линейны. Также линейными являются функции эквивалентность и сумма по модулю 2.
- Замкнутые классы. Монотонные функции.
Определение. Множество 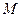 логических функций называется замкнутым классом, если любая суперпозиция функций из множества
логических функций называется замкнутым классом, если любая суперпозиция функций из множества 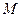 снова принадлежит
снова принадлежит 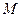 .
.
Всякая система 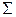 логических функций порождает некоторый замкнутый класс, а именно класс всех функций, которые можно получить суперпозициями функций
логических функций порождает некоторый замкнутый класс, а именно класс всех функций, которые можно получить суперпозициями функций 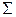 . Такой класс называется замыканием
. Такой класс называется замыканием 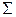 и обозначается
и обозначается 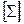 . Если множество
. Если множество 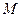 - функционально полная система, то
- функционально полная система, то 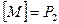 .
.
Пример 3.
а) Множество всех дизъюнкций, то есть функций вида 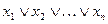 является замкнутым классом.
является замкнутым классом.
б) Множество всех линейных функций является замкнутым классом, так как подстановка формул вида 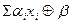 после преобразований даёт формулу такого же вида.
после преобразований даёт формулу такого же вида.
Важнейшим примером замкнутого класса является класс монотонных функций, который будет рассмотрен далее.
Ранее рассматривалось отношение частичного порядка 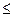 на множестве векторов одинаковой длины. Напомним, что для векторов
на множестве векторов одинаковой длины. Напомним, что для векторов 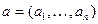 и
и 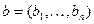 выполняется
выполняется 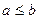 , если для любого
, если для любого 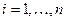 выполняется
выполняется 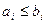 . Здесь воспользуемся этим отношением для двоичных векторов.
. Здесь воспользуемся этим отношением для двоичных векторов.
Определение. Функция 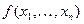 называется монотонной, если для любых двух двоичных наборов длины
называется монотонной, если для любых двух двоичных наборов длины 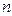 из того, что
из того, что 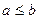 следует
следует 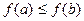 .
.
Пример 4.
а) Функция 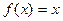 монотонна.
монотонна.
б) Дизъюнкция и конъюнкция любого числа переменных являются монотонными функциями.
в) Рассмотрим две функции от трёх переменных, заданных следующей таблицей.
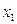
| 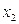
| 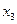
| 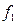
| 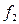
|
Функция 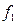 , очевидно, не является монотонной, так как, например
, очевидно, не является монотонной, так как, например 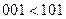 , а
, а 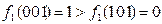 . Монотонность функции
. Монотонность функции 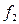 легко установить непосредственной проверкой.
легко установить непосредственной проверкой.
Дата добавления: 2015-08-11; просмотров: 1106;
