Два целых числа и называются сравнимыми по модулю , если при делении на это число они дают одинаковые остатки. 1 страница
Обозначается: 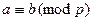 . Например,
. Например, 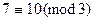 ,
,  . Так вот, функцию
. Так вот, функцию 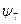 можно рассматривать, как сложение по модулю 2. Действительно, сумма остатков от деления чисел 0 и 1 на число 2 равна 1, а сумма остатков от деления чисел 0 и 0, либо 1 и 1 на 2 равна 0.
можно рассматривать, как сложение по модулю 2. Действительно, сумма остатков от деления чисел 0 и 1 на число 2 равна 1, а сумма остатков от деления чисел 0 и 0, либо 1 и 1 на 2 равна 0.
Функция 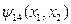 называется импликацией или логическим следованием. Обозначается:
называется импликацией или логическим следованием. Обозначается: 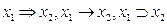 .
.
Функция 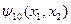 называется эквивалентностью или равнозначностью. Она равна 1, если значения переменных одинаковы и 0, если они различны. Обозначается:
называется эквивалентностью или равнозначностью. Она равна 1, если значения переменных одинаковы и 0, если они различны. Обозначается: 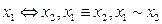 .
.
Есть ещё две функции двух переменных, имеющие специальные названия. Функция 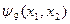 называется стрелкой Пирса и обозначается
называется стрелкой Пирса и обозначается 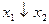 . Функция
. Функция 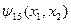 называется штрихом Шеффера и обозначается
называется штрихом Шеффера и обозначается 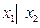 . Остальные функции специальных названий не имеют и, как можно показать, легко выражаются через перечисленные выше функции.
. Остальные функции специальных названий не имеют и, как можно показать, легко выражаются через перечисленные выше функции.
В функциях 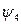 и
и 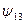 переменная
переменная 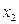 фиктивна. Из таблицы 3 видно, что
фиктивна. Из таблицы 3 видно, что 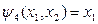 , а
, а 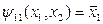 . Аналогично, в функциях
. Аналогично, в функциях 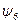 и
и 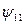 переменная
переменная 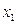 фиктивна:
фиктивна: 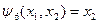 , а
, а 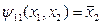 .
.
Доказано, что с ростом числа переменных 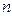 доля функций, имеющих фиктивные переменные, убывает и стремится к нулю.
доля функций, имеющих фиктивные переменные, убывает и стремится к нулю.
- Суперпозиции и формулы.
Ранее было введено определение суперпозиции функций, согласно которому суперпозицией нескольких функций называлась новая функция, полученная с помощью подстановок данных функцией друг в друга и переименования переменных. Выражение, описывающее эту суперпозицию, называли формулой. Поскольку понятие суперпозиции является очень важным в алгебре логики, рассмотрим его более подробно.
Пусть дано множество (конечное или бесконечное) исходных функций 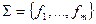 . Символы переменных
. Символы переменных 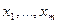 , содержащихся в данных функциях, будем считать формулами глубины 0.
, содержащихся в данных функциях, будем считать формулами глубины 0.
Определение. Говорят, что формула 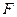 имеет глубину
имеет глубину 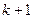 , если она имеет вид
, если она имеет вид 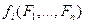 , где
, где 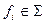 , а
, а 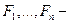 формулы, максимальная из глубин которых равна
формулы, максимальная из глубин которых равна 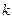 . При этом
. При этом 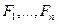 называются подформулами формулы
называются подформулами формулы 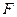 , а
, а 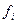 называется внешней, или главной операцией формулы
называется внешней, или главной операцией формулы 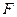 .
.
Соответственно, формулы 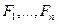 также могут иметь подформулы, которые являются в этом случае и подформулами формулы
также могут иметь подформулы, которые являются в этом случае и подформулами формулы 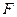 . Например, выражение
. Например, выражение 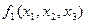 в наших обозначениях – это формула глубины 1. Выражение
в наших обозначениях – это формула глубины 1. Выражение 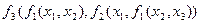 является формулой глубины 3, содержащей одну подформулу глубины 2 и две подформулы глубины 1.
является формулой глубины 3, содержащей одну подформулу глубины 2 и две подформулы глубины 1.
В дальнейшем конкретные формулы будем записывать в более привычном виде, при котором условные знаки функций стоят между аргументами (такую запись называют инфиксной). Например, если 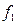 является конъюнкцией,
является конъюнкцией, 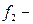 дизъюнкцией, а
дизъюнкцией, а 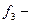 импликацией, то приведённая выше формула примет вид
импликацией, то приведённая выше формула примет вид 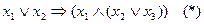 .
.
Все формулы, построенные подобным образом, то есть содержащие только символы переменных, скобки и знаки функций из множества 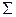 , называются формулами над множеством
, называются формулами над множеством 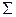 .
.
Возможны и другие интерпретации понятия глубины. Например, считается, что расстановка отрицаний над переменными не увеличивает глубины формулы. В случае, когда множество 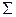 содержит некоторую ассоциативную операцию
содержит некоторую ассоциативную операцию 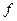 , можно считать, что применение этой операции к формулам с той же внешней операцией
, можно считать, что применение этой операции к формулам с той же внешней операцией 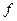 не увеличивает глубины формулы. Например, формулы
не увеличивает глубины формулы. Например, формулы 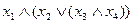 и
и 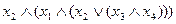 имеют одну и ту же глубину 3.
имеют одну и ту же глубину 3.
Всякая формула, выражающая данную функцию, как суперпозицию других функций, задаёт способ её вычисления (при условии, что известно, как вычислять исходные функции). Этот способ определяется следующим очевидным правилом: формулу можно вычислить, только если уже вычислены значения всех её подформул. Применим, например формулу 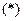 к набору
к набору 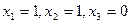 . Получим:
. Получим: 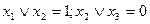 . Далее получим
. Далее получим 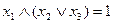 . Наконец,
. Наконец, 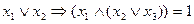 .
.
Таким образом, формула ставит в соответствие каждому набору значений аргументов значение функции и, значит, может наряду с таблицей служить способом задания и вычисления функции. В частности, по формуле, вычисляя её на всех 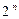 наборах, можно восстановить таблицу функции. О формуле, задающей функцию, говорят также, что она представляет или реализует функцию.
наборах, можно восстановить таблицу функции. О формуле, задающей функцию, говорят также, что она представляет или реализует функцию.
В отличие от табличного задания представление данной функции формулой не единственно. Например, если в качестве исходного множества функций зафиксировать функции 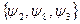 из предыдущего пункта (то есть функции И, ИЛИ, НЕ), то функцию
из предыдущего пункта (то есть функции И, ИЛИ, НЕ), то функцию 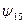 - штрих Шеффера – можно представить формулами
- штрих Шеффера – можно представить формулами 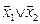 и
и 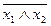 . Функцию
. Функцию 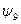 - стрелка Пирса – можно представить формулами
- стрелка Пирса – можно представить формулами 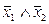 и
и 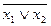 .
.
Определение. Формулы, представляющие одну и ту же функцию называются эквивалентными или равносильными.
Эквивалентность формул принято обозначать знаком равенства, поэтому можно записать: 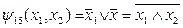 .
.
Существует стандартный метод для выяснения эквивалентности двух формул. По каждой формуле восстанавливается таблица функции, а затем две полученные таблицы сравниваются. Таким способом в предыдущеё лекции мы устанавливали равносильность высказываний. Он весьма громоздок, так как требует 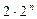 вычислений, если считать, что обе формулы зависят от
вычислений, если считать, что обе формулы зависят от 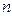 переменных. Более простыми методами, позволяющими устанавливать эквивалентность данных формул, а также получать новые формулы, эквивалентные исходной, являются эквивалентные преобразования, которые будут рассмотрены в дальнейшем.
переменных. Более простыми методами, позволяющими устанавливать эквивалентность данных формул, а также получать новые формулы, эквивалентные исходной, являются эквивалентные преобразования, которые будут рассмотрены в дальнейшем.
Лекция № 9. Булевы алгебры.
В данной лекции будут рассмотрены способы представления логических функций в виде суперпозиций функций И, ИЛИ, НЕ.
- Разложение функций по переменным. Совершенная дизъюнктивная нормальная форма.
Введём обозначения: 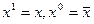 . Пусть
. Пусть 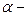 параметр, равный 0 или 1. Тогда
параметр, равный 0 или 1. Тогда 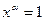 , если
, если 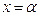 , и
, и 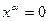 , если
, если 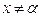 .
.
Теорема 8.1. Всякая логическая функция 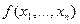 может быть представлена в следующем виде:
может быть представлена в следующем виде:
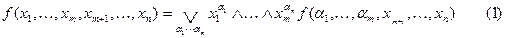 ,
,
где  , а дизъюнкция берётся по всем
, а дизъюнкция берётся по всем 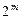 наборам значений переменных
наборам значений переменных 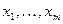 .
.
Равенство (1) называется разложением по переменным 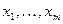 . Формула (1) достаточно громоздка на вид, однако её несложно использовать при небольших значениях
. Формула (1) достаточно громоздка на вид, однако её несложно использовать при небольших значениях 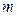 и
и 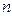 . Например, при значениях
. Например, при значениях 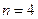 ,
, 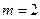 разложение (1) имеет вид:
разложение (1) имеет вид:
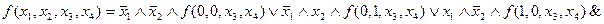
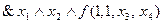 .
.
Практический смысл такого разложения очевиден: оно позволяет заменять функцию нескольких переменных суперпозицией конечного числа функций с меньшим количеством переменных. Особенно важен частный случай 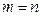 , когда разложение производится по всем переменным. При этом все переменные в правой части равенства (1) получают фиксированные значения, и функции в конъюнкциях правой части становятся равными 0 или 1, что даёт:
, когда разложение производится по всем переменным. При этом все переменные в правой части равенства (1) получают фиксированные значения, и функции в конъюнкциях правой части становятся равными 0 или 1, что даёт:
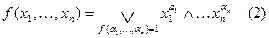 ,
,
где дизъюнкция берётся по всем наборам 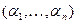 , на которых
, на которых 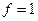 . Такое разложение называется совершенной дизъюнктивной нормальной формой (СДНФ) функции
. Такое разложение называется совершенной дизъюнктивной нормальной формой (СДНФ) функции 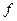 . СДНФ содержит ровно только конъюнкций, сколько единиц в таблице функции
. СДНФ содержит ровно только конъюнкций, сколько единиц в таблице функции 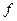 ; каждому единичному набору
; каждому единичному набору 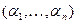 соответствует дизъюнкция всех переменных, в которых
соответствует дизъюнкция всех переменных, в которых 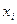 взято с отрицанием, если
взято с отрицанием, если  и без отрицания, если
и без отрицания, если 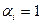 . Таким образом, существует взаимно однозначное соответствие между таблицей функции
. Таким образом, существует взаимно однозначное соответствие между таблицей функции 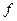 и её СДНФ. Следовательно, для каждой логической функции СДНФ является единственной (с точностью до порядка переменных и конъюнкций).
и её СДНФ. Следовательно, для каждой логической функции СДНФ является единственной (с точностью до порядка переменных и конъюнкций).
Пример 1. Составить СДНФ для функции, заданной таблицей:
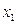
| 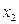
| 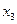
| 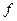
|
Поскольку данная таблица (уже встречавшаяся ранее) содержит три единичных набора, СДНФ будет конъюнкцией трёх дизъюнкций. В свою очередь, каждая дизъюнкция включает три переменных – по числу их в функции 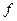 .
.
Получим: 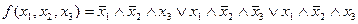 .
.
Напомним, что, подобно знаку умножения, знак дизъюнкции 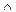 в логических формулах часто опускают. Тогда полученное выражение примет более компактный вид:
в логических формулах часто опускают. Тогда полученное выражение примет более компактный вид:
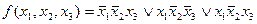 .
.
Единственная функция, которая не имеет СДНФ – это константа 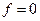 .
.
Формулы, содержащие кроме переменных и скобок, только знаки дизъюнкции, конъюнкции и отрицания, будем называть булевыми формулами.
Теорема 8.2. Всякая логическая функция может быть представлена булевой функцией, то есть как суперпозиция дизъюнкции, конъюнкции и отрицания.
- Булева алгебра функций.
Выше мы обозначили множество всех логических операций на двухэлементном множестве 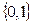 , как
, как 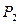 .
.
Определение. Булевой алгеброй логических функций называется алгебра вида 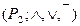 , основным множеством которой является всё множество логических функций, а операциями – дизъюнкция, конъюнкция и отрицание.
, основным множеством которой является всё множество логических функций, а операциями – дизъюнкция, конъюнкция и отрицание.
Замечание. На практике мы имеем дело не самими функциями, а с представляющими их формулами, то есть с алгеброй формул, которая значительно шире, поскольку каждую функцию представляет бесконечное множество формул. Чтобы “синхронизировать” их алгебре формул придаётся следующий вид. Элементами алгебры формул объявляются не сами формулы, а классы эквивалентности формул, то есть классы формул, представляющих одну и ту же функцию. Определённая таким образом, алгебра формул называется алгеброй Линденбаума - Тарского. Она изоморфна булевой алгебре функций.
Теперь рассмотрим основные свойства булевых операций (частично уже знакомые по теме “Элементы математической логики”).
1. Ассоциативность: а) 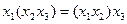 ; б)
; б) 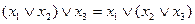 .
.
2. Коммутативность: а) 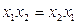 ; б)
; б) 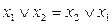 .
.
3. Дистрибутивность конъюнкции относительно дизъюнкции: 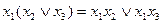 .
.
4. Дистрибутивность дизъюнкции относительно конъюнкции:
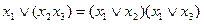 .
.
5. Идемпотентность: а) 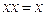 ; б)
; б) 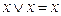 .
.
6. Двойное отрицание: 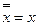 .
.
7. Свойства констант: а) 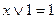 ; б)
; б) 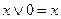 ; в)
; в) 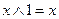 ; г)
; г) 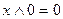 ; д)
; д) 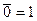 ; е)
; е) 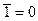 .
.
8. Правила де Моргана: а) 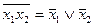 ; б)
; б) 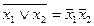 . Очень важные соотношения, которые часто будут использоваться в дальнейшем. С их помощью (а также с помощью соотношения 6) дизъюнкция заменяется конъюнкцией и наоборот.
. Очень важные соотношения, которые часто будут использоваться в дальнейшем. С их помощью (а также с помощью соотношения 6) дизъюнкция заменяется конъюнкцией и наоборот.
9. Закон противоречия: 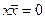 .
.
10. Закон “исключённого третьего”: 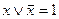 .
.
Все соотношения 1 – 10 можно проверить указанным ранее стандартным методом – вычислением обеих частей равенств на всех наборах значений переменных. Эти равенства остаются справедливыми и в случае подстановки вместо переменной любой логической функции и, следовательно, любой формулы, представляющей эту функцию. Важно лишь соблюдать следующее правило подстановки формулы вместо переменной.
При подстановке формулы 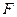 вместо переменной
вместо переменной 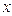 всевхождения данной переменной в исходное соотношение должны быть одновременно заменены формулой
всевхождения данной переменной в исходное соотношение должны быть одновременно заменены формулой 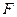 .
.
Правило подстановки позволяет получать из соотношений 1 – 10 новые эквивалентные соотношения. Заметим, что равенство 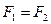 означает в данном контексте, что формулы
означает в данном контексте, что формулы 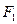 и
и 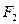 описывают одну и ту же логическую функцию. Следовательно, если какая-то формула
описывают одну и ту же логическую функцию. Следовательно, если какая-то формула 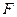 содержит
содержит 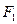 в качестве подформулы, то замена её на
в качестве подформулы, то замена её на 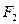 не изменит значения формулы
не изменит значения формулы 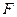 . Это утверждение представляет собой правило замены подформул, которое позволяет, используя эквивалентные соотношения, получать формулы, эквивалентные данной. Практическое применение описанных правил будет рассмотрено ниже.
. Это утверждение представляет собой правило замены подформул, которое позволяет, используя эквивалентные соотношения, получать формулы, эквивалентные данной. Практическое применение описанных правил будет рассмотрено ниже.
Замечание. Есть существенная разница между подстановкой и заменой. При подстановке переменная заменяется формулой; при этом формула может быть любой, лишь бы производилась одновременная замена ею всех вхождений переменной. При замене подформул может быть заменена любая подформула, однако, не на любую другую, а только на подформулу, эквивалентную ей. При этом замена всех вхождений исходной подформулы не обязательна.
- Эквивалентные преобразования.
Пример 2. Возьмём соотношение 8а и подставим вместо переменной 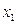 выражение
выражение 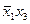 . Получим:
. Получим: 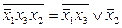 . Здесь в обеих частях стоят формулы, неэквивалентные исходным формулам, но эквивалентные между собой. Если же в правой части нового соотношения формулу
. Здесь в обеих частях стоят формулы, неэквивалентные исходным формулам, но эквивалентные между собой. Если же в правой части нового соотношения формулу 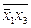 заменить формулой
заменить формулой  , эквивалентной ей в силу соотношения 8а и затем заменить
, эквивалентной ей в силу соотношения 8а и затем заменить 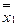 на
на 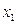 (согласно 6), то получим
(согласно 6), то получим 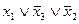 . Причём все формулы в полученной цепи преобразований являются эквивалентными:
. Причём все формулы в полученной цепи преобразований являются эквивалентными:
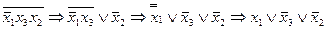 .
.
Такие преобразования, использующие эквивалентные соотношения и правило замены, называют эквивалентными преобразованиями. Эквивалентные преобразования являются мощным средством доказательства эквивалентности формул, как правило, более эффективным, чем их вычисление на наборах значений переменных.
В булевой алгебре принято опускать скобки в следующих двух случаях: а) при последовательном выполнении нескольких конъюнкций или дизъюнкций; б) если они являются внешними скобками у конъюнкции. Оба соглашения совершенно аналогичны общепринятому опусканию скобок для операции умножения в арифметических выражениях.
Рассмотрим несколько способов упрощения формул с помощью эквивалентных преобразований, позволяющих получить формулы, содержащие меньшее количество символов.
а) Поглощение: 1) 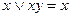 и 2)
и 2) 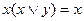 . Докажем данное равенство подробно, используя для доказательства соотношения 3, 7а и 7в.
. Докажем данное равенство подробно, используя для доказательства соотношения 3, 7а и 7в.
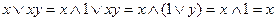 .
.
Далее будем опускать доказательства приводимых равенств, которые при желании можно получить из соотношений 1 – 10 и уже доказанных равенств.
б) Склеивание: 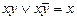 .
.
в) Обобщённое склеивание: 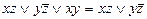 .
.
г) 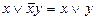 .
.
Одним из главных видов упрощения формул является приведение их к дизъюнктивной нормальной форме (ДНФ).
Определение. Элементарными конъюнкциями называются конъюнкции переменных или их отрицаний, в которых каждая переменная встречается не более одного раза. Дизъюнктивной нормальной формой называется формула, имеющая вид дизъюнкции элементарных конъюнкций.
Заметим, что СДНФ является частным случаем ДНФ.
Приведение формулы к ДНФ выполняется так. Сначала с помощью соотношений 6 и 8 все отрицания “спускаются” до переменных. Затем раскрываются скобки. После этого с помощью соотношений 5, 9 и 10 удаляются лишние конъюнкции и повторения переменных в конъюнкциях. Наконец, с помощью соотношений 7а – 7е удаляются лишние константы. При этом необходимо помнить, что ДНФ данной формулы может быть не единственной.
Пример 3. Привести к ДНФ формулу 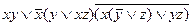 .
.
Решение:

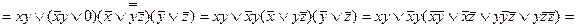
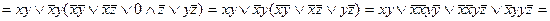
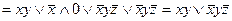 . В итоге получили дизъюнкцию элементарных конъюнкций, то есть ДНФ.
. В итоге получили дизъюнкцию элементарных конъюнкций, то есть ДНФ.
Доказано, что если из формулы 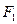 можно с помощью эквивалентных преобразований получить формулу
можно с помощью эквивалентных преобразований получить формулу 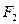 , то можно из формулы
, то можно из формулы 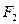 (с помощью тех же соотношений) получить формулу
(с помощью тех же соотношений) получить формулу 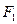 . Иначе говоря, всякое эквивалентное преобразование обратимо. Это позволяет сформулировать следующую теорему.
. Иначе говоря, всякое эквивалентное преобразование обратимо. Это позволяет сформулировать следующую теорему.
Теорема 8.3. Для любых двух эквивалентных формул 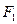 и
и 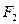 существует эквивалентное преобразование
существует эквивалентное преобразование 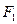 в
в 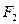 и наоборот с помощью соотношений 1 – 10.
и наоборот с помощью соотношений 1 – 10.
Аналогично понятию ДНФ определяется понятие конъюнктивной нормальной формы (КНФ), то есть КНФ есть конъюнкция элементарных дизъюнкций. Переход от КНФ к ДНФ и обратно всегда осуществим (обычно, с помощью формул Де Моргана).
Пример 4. Привести формулу 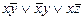 к КНФ.
к КНФ.
Заменим исходную формулу её двойным отрицанием, а затем применим соотношения 8.

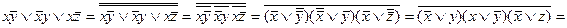
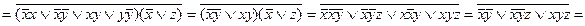
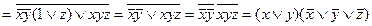 .
.
Лекция № 10. Булевы алгебры и теория множеств.
- Двойственность.
Определение. Функция 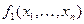 называется двойственной к функции
называется двойственной к функции  , если
, если 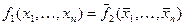 .
.
Если взять отрицание обеих частей равенства и подставить 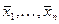 вместо переменных
вместо переменных 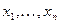 , то получится
, то получится 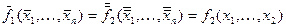 . Это означает, что функция
. Это означает, что функция 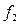 двойственна к функции
двойственна к функции 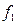 , и, таким образом, отношение двойственности является симметричным. Из определения двойственности ясно, что для любой функции двойственная ей функция определяется однозначно. В частности, может оказаться, что функция двойственна самой себе. В этом случае она называется самодвойственной.
, и, таким образом, отношение двойственности является симметричным. Из определения двойственности ясно, что для любой функции двойственная ей функция определяется однозначно. В частности, может оказаться, что функция двойственна самой себе. В этом случае она называется самодвойственной.
Дата добавления: 2015-08-11; просмотров: 1008;
