РАЗДЕЛ IV. ТЕОРИЯ ГРАФОВ.
Лекция № 14. Графы: основные понятия и операции.
Теорию графов начали разрабатывать для решения некоторых задач о геометрических конфигурациях, состоящих из точек и линий. В дальнейшем оказалось, что понятие графа можно применять не только при исследовании геометрических конфигураций. Особенно часто определяют графы при анализе функционирование неких систем.
- Графы, их вершины, рёбра и дуги. Изображение графов.
Определение. Если на плоскости задать конечное множество V точек и конечный набор линий E, соединяющих некоторые пары из точек V, то полученная совокупность точек и линий будет называться графом G = (V, E).
При этом элементы множества V называются вершинами графа, а элементы множества E – ребрами.
Определение. Если вершина v является концом ребра 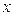 , то говорят, что v и
, то говорят, что v и 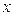 инцидентны.
инцидентны.
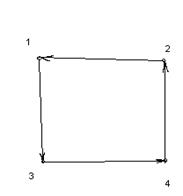
В множестве V могут встречаться одинаковые элементы, ребра, соединяющие одинаковые элементы называются петлями (на рисунке 1.4 при вершине 5 имеется петля). Одинаковые пары в множестве E называются кратными (или параллельными) ребрами. Количество одинаковых пар (v, w) в E называется кратностьюребра (v, w). Например, на рисунке 1.1 все рёбра имеют кратность 1, а на рисунке 1.2 есть два ребра, соединяющих одни и те же вершины 1 и 4, следовательно, их кратность равна двум.
Множество V и набор E определяют граф с кратными ребрами – псевдограф.
Псевдограф без петель называется мультиграфом.
Если в наборе E ни одна пара не встречается более одного раза, то мультиграф называется графом.
Ниже, на рисунке 1.1 изображен граф, на рисунке 1.2 мультиграф, на рисунке 1.4 – псевдограф.
Графу соответствует геометрическая конфигурация. Вершины обозначаются точками (кружочками), а ребра – линиями, соединяющими соответствующие вершины. На рисунке 1 изображены некоторые неориентированные графы.
Рисунок 1.
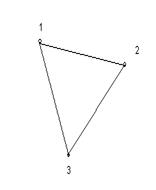
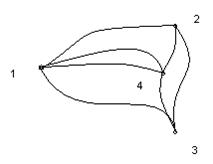
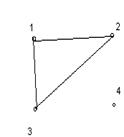
1.1 1.2 1.3
1.4 1.5
Замечание 1. Слово “линия”, которое мы используем, подразумевает несущественность того, какая конкретно линия используется для соединения двух вершин графа, то есть её геометрические характеристики не имеют значения.
Замечание 2. Граф можно определить, также как совокупность двух множеств  и
и 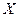 , между элементами которых установлено отношение инцидентности, при котором каждый элемент
, между элементами которых установлено отношение инцидентности, при котором каждый элемент  инцидентен ровно двум элементам
инцидентен ровно двум элементам 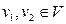 .
.
Определение. Если х = {v, w} – ребро графа, то вершины v, w называются концами ребра х.
Определение. Если пары в наборе E являются упорядоченными, то граф называется ориентированным или орграфом.
Если пишут 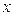 = (v, w) – дуга орграфа, то вершина v – начало, а вершина w – конец дуги х.
= (v, w) – дуга орграфа, то вершина v – начало, а вершина w – конец дуги х.
Определение. Вершины v, w графа G = (V, E) называются смежными, если {v,w}ÎЕ. Два ребра называются смежными, если они имеют общую вершину.
Определение.Степенью вершины графа называется число ребер, которым эта вершина принадлежит. Вершина называется висячей, если ее степень равна единице и изолированной, если ее степень равна нулю.
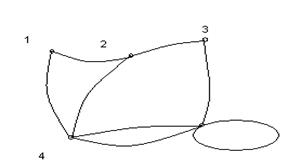
На рисунке 1.5 все вершины, кроме вершины 1, являются висячими. На рисунке 1.3 вершина 4 является изолированной. Если граф состоит только из таких вершин, его называют пустым. В некоторых случаях пустым называют граф, не имеющей ни одной вершины.
Рисунок 2.

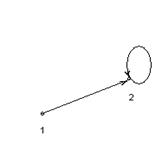
2.1 2.2 2.3
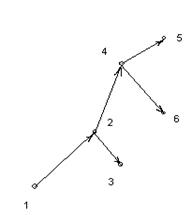
a. 2.5
На рисунке 2 представлены различные типы ориентированных графов.
Заметим, что каждому неориентированному графу можно поставить в соответствие ориентированный граф с тем же множеством вершин, в котором каждое ребро заменено двумя противоположными рёбрами, инцидентными тем же вершинам. Такое соответствие называется каноническим.
- Матрица инцидентности и список рёбер. Матрица смежности графа.
Обычно рассматриваемые графы конечны, то есть, конечны множества их элементов – вершин и рёбер. Поэтому в дальнейшем конечность графов не будет оговариваться, тем более, что важнейшие понятия и результаты, приводимые ниже относятся к произвольным графам.
Задать граф – значит, описать множества его вершин и рёбер и задать между ними отношение инцидентности. Когда граф 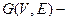 конечный, для описания его вершин и рёбер достаточно их занумеровать. Пусть
конечный, для описания его вершин и рёбер достаточно их занумеровать. Пусть 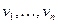 - вершины графа, а
- вершины графа, а 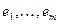 - его рёбра. Отношение инцидентности можно определить матрицей
- его рёбра. Отношение инцидентности можно определить матрицей 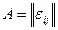 размерности
размерности 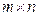 . Столбцы этой матрицы будут соответствовать вершинам графа, а строки – его рёбрам. Если ребро
. Столбцы этой матрицы будут соответствовать вершинам графа, а строки – его рёбрам. Если ребро 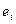 инцидентно вершине
инцидентно вершине 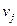 , то
, то 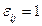 , в противном случае -
, в противном случае - 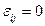 . Такая матрица называется матрицей инцидентности неориентированного графа, поскольку по способу её задания невозможно различить начало и конец каждого ребра.
. Такая матрица называется матрицей инцидентности неориентированного графа, поскольку по способу её задания невозможно различить начало и конец каждого ребра.
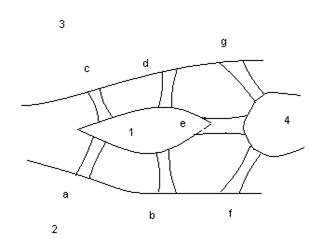
Пример 1. Составить матрицу инцидентности неориентированного графа, изображённого на рисунке 3.
Рисунок 3.
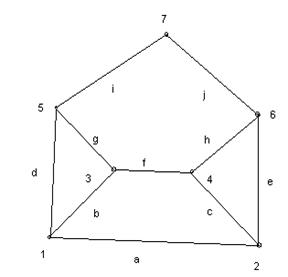
Строим матрицу инцидентности в виде таблицы:
| a | |||||||
| b | |||||||
| c | |||||||
| d | |||||||
| e | |||||||
| f | |||||||
| g | |||||||
| h | |||||||
| i | |||||||
| j |
Для ориентированного графа матрица инцидентности составляется иначе. Это матрица 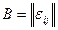 размерности
размерности 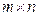 .
.
Если вершина 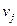 - начало ребра
- начало ребра 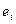 , то
, то 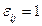 . Если вершина
. Если вершина 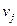 - конец ребра
- конец ребра 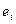 , то
, то 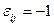 . Если вершине
. Если вершине 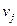 инцидентна петля
инцидентна петля 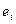 , то
, то 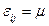 , где
, где  любое число, кроме чисел
любое число, кроме чисел 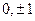 (обычно берут 2). В любом противном случае -
(обычно берут 2). В любом противном случае - 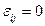 .
.
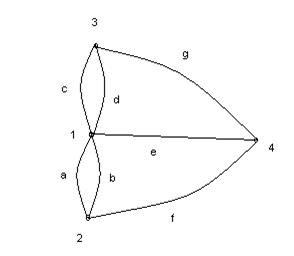
Пример 2. Построить матрицу инцидентности для графа, изображённого на рисунке 4.

Строим матрицу инцидентности в виде таблицы:
| a | -1 | ||||||
| b | -1 | ||||||
| c | -1 | ||||||
| d | -1 | ||||||
| e | -1 | ||||||
| f | -1 | ||||||
| g |
Ещё проще задавать граф с помощью таблицы рёбер. Она состоит из двух столбцов; в левых содержатся названия рёбер, а в правых – инцидентные им вершины (для ориентированных графов обязательно сначала указывается начало ребра, потом конец). Ниже приведены таблицы рёбер для графов из примеров 1 и 2.
Для примера 1:
| Рёбра | Вершины |
| a | 1, 2 |
| b | 1, 3 |
| c | 2, 4 |
| d | 1, 5 |
| e | 2, 6 |
| f | 3, 4 |
| g | 3, 5 |
| g | 4, 6 |
| i | 5, 7 |
| j | 6, 8 |
Для примера 2:
| Рёбра | Вершины |
| a | 1, 2 |
| b | 1, 3 |
| c | 2, 4 |
| d | 3, 5 |
| e | 3, 6 |
| f | 3, 7 |
| g | 7, 7 |
Очевидно, по списку рёбер можно построить его таблицу инцидентности. Действительно, каждая строка этого списка соответствует строке матрицы с тем же номером; аналогично можно выполнить обратную процедуру.
Ещё одним способом представления графа является построение для него матрицы смежности. Это квадратная матрица 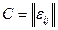 , в которой количество строк и столбцов равно количеству вершин графа. Для неориентированного графа
, в которой количество строк и столбцов равно количеству вершин графа. Для неориентированного графа 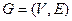 эта матрица определяется следующим образом. Если вершины
эта матрица определяется следующим образом. Если вершины 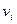 и
и 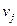 являются смежными, то есть если выполняется
являются смежными, то есть если выполняется 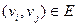 , то
, то 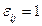 . В противном случае,
. В противном случае, 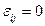 . Для графа из примера 1 таблица смежности имеет вид:
. Для графа из примера 1 таблица смежности имеет вид:
Матрица смежности неориентированного графа обязательно симметрична. Размерность матрицы указывает на количество вершин, а число рёбер равно половине единиц, имеющихся в матрице.
Матрица смежности ориентированного графа отличается только тем, что 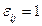 в том и только в том случае, когда в паре смежных вершин
в том и только в том случае, когда в паре смежных вершин 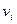 и
и 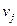 вершина
вершина 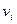 является началом, а вершина
является началом, а вершина 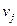 - концом ребра. Для графа из примера 2 матрица смежности выглядит следующим образом:
- концом ребра. Для графа из примера 2 матрица смежности выглядит следующим образом:
Очевидно, что вся информация об ориентированном графе, порождающем некоторую матрицу смежности, содержится в верхнем (относительно главной диагонали) её треугольнике.
Ориентированный граф с симметричной матрицей смежности канонически соответствует неориентированному графу, имеющему ту же таблицу смежности (но не наоборот).
- Идентификация графов, заданных своими представлениями.
Итак, граф может быть представлен различными способами. Он может быть задан рисунком, матрицей инцидентности, списком рёбер или матрицей смежности. Вид чертежа зависит от формы линий и взаимного расположения вершин. Иногда, даже для пары достаточно простых графов, непонятно, одинаковы ли они (см. рисунок 5 “а” и “б”). Вид матриц, также как списков рёбер зависит от нумерации вершин и рёбер графа. В связи с этим возникает весьма существенный вопрос о том, как определять равенство графов.
Рисунок 5.
а) 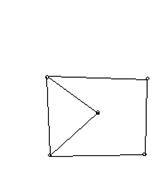 б)
б)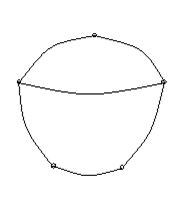
Строго говоря, граф считается полностью заданным, если нумерация его вершин зафиксирована. Графы, отличающиеся только нумерацией вершин, называются изоморфными.
Определение.Графы G1(V1, E1) и G2(V2, E2) называются изоморфными, если существует взаимно однозначное отображение j: V1 ® V2, сохраняющее смежность.
Перенумерация вершин графа задаётся строкой 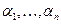 новых номеров вершин, расположенных в исходном порядке. Новая матрица смежности получается из исходной матрицы перемещением каждого элемента
новых номеров вершин, расположенных в исходном порядке. Новая матрица смежности получается из исходной матрицы перемещением каждого элемента 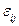 в
в 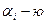 строку, в
строку, в  столбец. Поэтому, чтобы узнать, представляют ли две таблицы смежности изоморфные графы, можно, например, перевести всевозможные одинаковые перестановки строк и столбцов первой матрицы. Если одна из таких перестановок даст матрицу, тожественно совпадающую со второй матрицей, то представляемые ими графы изоморфны. Однако эта процедура может оказаться очень трудоёмкой, так как всего возможно выполнение
столбец. Поэтому, чтобы узнать, представляют ли две таблицы смежности изоморфные графы, можно, например, перевести всевозможные одинаковые перестановки строк и столбцов первой матрицы. Если одна из таких перестановок даст матрицу, тожественно совпадающую со второй матрицей, то представляемые ими графы изоморфны. Однако эта процедура может оказаться очень трудоёмкой, так как всего возможно выполнение 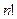 перестановок.
перестановок.
Лекция № 15. Маршруты, цепи и циклы.
- Основные определения.
Пусть G(V, Е) – неориентированный граф. Рассмотрим конечную последовательность рёбер 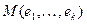 такую, что любые два соседние ребра
такую, что любые два соседние ребра 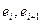 имеют одну общую инцидентную вершину
имеют одну общую инцидентную вершину  . Эту последовательность называется маршрутом графа.
. Эту последовательность называется маршрутом графа.
Определение . Маршрутом (путем) для графа G(V, Е) называется последовательность v1e1v2e2v3…ekvk+1. Маршрут называется замкнутым, если его начальная и конечная точки совпадают. Число ребер (дуг) маршрута (пути) графа называется длиноймаршрута (пути).
Любой отрезок конечного или бесконечного маршрута 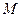 вида
вида 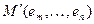 , где
, где 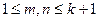 также является маршрутом и называется участком маршрута
также является маршрутом и называется участком маршрута 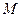 .
.
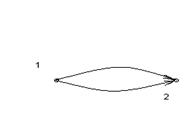
Заметим, что одно и то же ребро может встречаться не один раз. Вершина 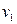 , инцидентная первому ребру маршрута
, инцидентная первому ребру маршрута 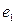 и не инцидентная следующему ребру
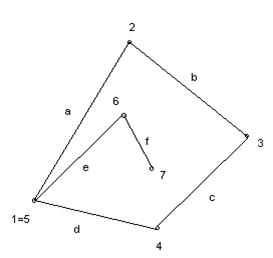
и не инцидентная следующему ребру 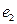 , называется началом маршрута. Причём если эти рёбра кратные, то необходимо указать, какая именно из двух инцидентных им вершин является началом маршрута. Аналогично определяется конец маршрута. Вершины, инцидентные рёбрам маршрута, за исключением первой и последней, называются промежуточными. Причём, поскольку одной вершине может быть инцидентно несколько рёбер, начало и конец маршрута могут быть в то же время промежуточными точками. Таков, например, маршрут
, называется началом маршрута. Причём если эти рёбра кратные, то необходимо указать, какая именно из двух инцидентных им вершин является началом маршрута. Аналогично определяется конец маршрута. Вершины, инцидентные рёбрам маршрута, за исключением первой и последней, называются промежуточными. Причём, поскольку одной вершине может быть инцидентно несколько рёбер, начало и конец маршрута могут быть в то же время промежуточными точками. Таков, например, маршрут  на рисунке 1, где вершина 1 является началом маршрута и, в то же время, промежуточной точкой.
на рисунке 1, где вершина 1 является началом маршрута и, в то же время, промежуточной точкой.
Рисунок 1.
Рассмотрим случай, когда 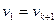 , то есть начало и конец маршрута совпадают. Отметим, что в этом случае маршрут может быть только конечным..
, то есть начало и конец маршрута совпадают. Отметим, что в этом случае маршрут может быть только конечным..
Определение. Незамкнутый маршрут (путь) называется цепью. Цепь, в которой все вершины попарно различны, называется простой цепью.
В простой цепи любая вершина маршрута инцидентна не более чем двум его рёбрам.
Определение. Замкнутый маршрут (путь) называется циклическим маршрутом или циклом (контуром). Цикл, в котором все вершины попарно различны, называется простым циклом.
Иначе говоря, простой цикл – это циклический маршрут, в котором любые два соседние ребра имеют одну инцидентную вершину. Последовательности 
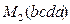 ,
, 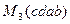 и
и 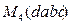 представляют один и тот же цикл (рисунок 2). Часто считается, что можно менять порядок рёбер цикла на противоположный, то есть, например, последовательность
представляют один и тот же цикл (рисунок 2). Часто считается, что можно менять порядок рёбер цикла на противоположный, то есть, например, последовательность 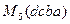 представляет тот же цикл.
представляет тот же цикл.
Рисунок 2.
Участок цепи или цикла является цепью; соответственно, участок простой цепи или простого цикла является простой цепью.
- Связные компоненты графов.
Определение. Вершины 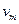 и
и  называются связанными, если существует маршрут
называются связанными, если существует маршрут 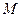 с началом
с началом 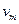 и концом
и концом  . Наоборот, маршрут
. Наоборот, маршрут 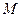 с началом
с началом 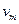 и концом
и концом  называется связывающим эти вершины.
называется связывающим эти вершины.
Очевидно, что при существовании маршрута 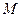 должен также существовать маршрут
должен также существовать маршрут 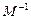 с началом
с началом  и концом
и концом 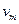 , в котором рёбра идут в противоположном порядке. Можно показать, что любые две связанные маршрутом
, в котором рёбра идут в противоположном порядке. Можно показать, что любые две связанные маршрутом 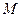 вершины можно связать маршрутом
вершины можно связать маршрутом 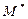 , являющимся простой цепью, состоящей из участков маршрута
, являющимся простой цепью, состоящей из участков маршрута 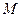 .
.
Если вершина 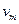 связана с какой-то вершиной
связана с какой-то вершиной 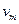 маршрутом
маршрутом 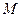 , то она, естественно связана с собой маршрутом, состоящим из маршрутов
, то она, естественно связана с собой маршрутом, состоящим из маршрутов 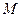 и
и 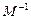 . Более того, принято считать, что изолированная вершина также связана сама с собой, то есть отношение связности, заданное на множестве вершин данного графа
. Более того, принято считать, что изолированная вершина также связана сама с собой, то есть отношение связности, заданное на множестве вершин данного графа 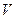 рефлексивно. Оно также симметрично и транзитивно, а поэтому является отношением эквивалентности. Тогда оно порождает разбиение множества
рефлексивно. Оно также симметрично и транзитивно, а поэтому является отношением эквивалентности. Тогда оно порождает разбиение множества 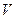 на непересекающиеся подмножества такие, что вершины одного подмножества
на непересекающиеся подмножества такие, что вершины одного подмножества 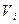 связаны между собой и не связаны с вершинами другого подмножества
связаны между собой и не связаны с вершинами другого подмножества 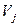 . Это, в свою очередь, означает, что граф может быть разложен в прямую сумму подграфов:
. Это, в свою очередь, означает, что граф может быть разложен в прямую сумму подграфов:  .
.
Определение. Граф называется связным, если все его вершины связаны между собой.
Поэтому все подграфы связного графа 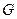 связны и называются связными компонентами графа
связны и называются связными компонентами графа 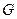 .
.
- Расстояния. Диаметр, радиус и центр графа. Протяжённости.
Пусть 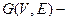 связный неориентированный граф,
связный неориентированный граф, 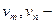 любые две его вершины. Тогда существует связывающая их простая цепь
любые две его вершины. Тогда существует связывающая их простая цепь 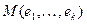 . Если количество этих рёбер
. Если количество этих рёбер 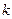 - не минимальное из возможных, существует цепь
- не минимальное из возможных, существует цепь 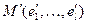 , причём
, причём 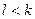 .
.
Штрихи в обозначении используются, потому что не обязательно рёбра под одинаковыми индексами будут совпадать.
Если же и 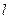 не минимально, то найдётся связывающая эти вершины цепь
не минимально, то найдётся связывающая эти вершины цепь 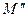 с ещё меньшим количеством рёбер и так далее. Однако этот процесс не бесконечен, его можно повторить не более, чем
с ещё меньшим количеством рёбер и так далее. Однако этот процесс не бесконечен, его можно повторить не более, чем 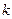 раз. Тогда существует цепь
раз. Тогда существует цепь 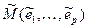 связывающая вершины
связывающая вершины 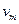 и
и  с минимальным количеством рёбер
с минимальным количеством рёбер 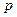 .
.
Определение. Минимальная длина простой цепи с началом в вершине 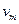 и концом в вершине
и концом в вершине  называется расстоянием между этими вершинами. Обозначается:
называется расстоянием между этими вершинами. Обозначается: 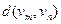 .
.
Расстояние 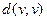 между любой вершиной и ею самой равно 0. Ему соответствует нулевой маршрут, не содержащий рёбер. Для любой пары различных вершин
между любой вершиной и ею самой равно 0. Ему соответствует нулевой маршрут, не содержащий рёбер. Для любой пары различных вершин 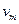 и
и  выполняется
выполняется 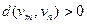 , так как связывающая их цепь состоит хотя бы из одного ребра. Вообще, расстояние
, так как связывающая их цепь состоит хотя бы из одного ребра. Вообще, расстояние 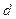 удовлетворяет аксиомам метрики:
удовлетворяет аксиомам метрики:
1) 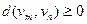 , причём
, причём 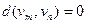 тогда и только тогда, когда
тогда и только тогда, когда 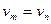 ;
;
2) 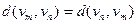 .
.
Также для расстояния 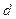 выполняется неравенство треугольника: для любых трёх вершин
выполняется неравенство треугольника: для любых трёх вершин  выполняется неравенство:
выполняется неравенство: 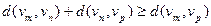 .
.
Это позволяет, для простоты рассуждений, измерять расстояние между вершинами по числу рёбер простой цепи, соединяющей их (тем более, что геометрические характеристики рёбер мы не учитываем)..
Определение. Диаметром конечного графа 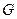 называется наибольшее из расстояний между парой его вершин:
называется наибольшее из расстояний между парой его вершин: 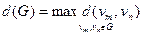 .
.
Кратчайшие простые цепи, связывающие две вершины графа с максимальным расстоянием между ними, называются диаметральными простыми цепями.
Пусть 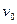 - рассматриваемая вершина данного графа, а
- рассматриваемая вершина данного графа, а 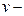 произвольная вершина графа. Максимальным удалением в графе
произвольная вершина графа. Максимальным удалением в графе 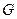 от фиксированной вершины
от фиксированной вершины 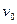 называется величина
называется величина 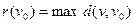 .
.
Определение. Вершина 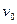 называется центром графа
называется центром графа 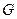 , если максимальное удаление от неё до остальных вершин графа принимает минимальное значение:
, если максимальное удаление от неё до остальных вершин графа принимает минимальное значение: 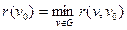 .
.
Максимальное удаление от центра графа называется его радиусом и обозначается 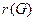 , а любая кратчайшая цепь от центра до наиболее удаленной от него вершины - радиальной цепью.
, а любая кратчайшая цепь от центра до наиболее удаленной от него вершины - радиальной цепью.
Замечание. Граф может иметь более одного центра. Например, в полном неориентированном графе, в котором две любые различные вершины соединены ребром, радиус равен единице, а любая вершина является центром.
Пусть 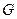 - конечный, связный граф, число рёбер которого равно
- конечный, связный граф, число рёбер которого равно 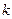 . Из соображений, изложенных при изучении комбинаторики, можно сделать очевидный вывод. Количество последовательностей рёбер этого графа конечно и равно
. Из соображений, изложенных при изучении комбинаторики, можно сделать очевидный вывод. Количество последовательностей рёбер этого графа конечно и равно 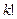 . Следовательно, конечно и количество простых цепей, в которых рёбра не повторяются.
. Следовательно, конечно и количество простых цепей, в которых рёбра не повторяются.
Определение. Протяжённостью 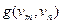 называется максимальная из длин связывающих эти вершины простых цепей.
называется максимальная из длин связывающих эти вершины простых цепей.
- Эйлеровы графы.
Определение. Цепь (цикл) в графе G называется Эйлеровым, если она проходит по одному разу через каждое ребро графа G.
Теорема 15.1. Для того, чтобы связный граф G обладал Эйлеровым циклом, необходимо и достаточно, чтобы степени его вершин были четными.
Рисунок 3
а) б)
Задача, которая привела к появлению понятия Эйлерова цикла, широко известна в истории математики. Это так называемая задача о кенигсбергских мостах. Расположение семи мостов в городе Кенигсберге в начале XVIII века приведено на рисунке 3а. Требуется обойти город, пройдя через каждый мост ровно один раз, и вернуться в исходную точку.
Можно представить описанную задачу следующим образом. Имеется связный неориентированный граф с четырьмя вершинами и семью рёбрами. Требуется выяснить, существует ли простой цикл, позволяющий обойти данный граф по маршруту, включающему в себя по одному разу каждое ребро графа.
Именно решение данной задачи привело Л. Эйлера к доказательству приведённой выше теоремы. Кстати, согласно ей, данная задача неразрешима, поскольку степени всех вершин графа нечётны.
Теорема 15.2. Для того, чтобы связный граф G обладал Эйлеровой цепью, необходимо и достаточно, чтобы он имел ровно две вершины нечетной степени.
По сути дела, теоремы 15.1 и 15.2 описывают условия, при которых можно построить геометрическую фигуру “не отрывая карандаша от бумаги”, одной сплошной линией. Только в первом случае начало и конец этой линии будут совпадать, а во втором случае они будут различны.
Определение. Цикл (цепь) в графе G называется Гамильтоновым, если он проходит через каждую вершину графа G ровно один раз.
Пример 1.

а)
- в графе есть и Эйлеров и Гамильтонов циклы

б)
- в графе есть Эйлеров цикл, но нет Гамильтонова
в)
- в графе есть гамильтонов, но нет Эйлерова цикла
г)
- в графе нет ни Эйлерова, ни Гамильтонова цикла
Граф G называется полным, если каждая его вершина является смежной со всеми остальными вершинами. В полном графе всегда существуют гамильтоновы циклы.
Также необходимым условием существования гамильтонова цикла является связность графа.
Лекция № 16. Некоторые классы графов и их частей.
- Деревья.
Определение. Связный неориентированный граф без циклов называется неориентированным деревом или просто деревом.
Из определения следует, что дерево не может содержать ни петель, ни кратных рёбер.
Определение. Несвязный неориентированный граф без циклов называется лесом; связные компоненты леса являются деревьями.
Очевидно, что люба часть дерева или леса также не имеет циклов. В таком графе любая цепь является простой – в противном случае, она содержала бы цикл.
Теорема 16.1. Любые две вершины дерева связаны одной и только одной цепью. Обратно, если две любые вершины графа можно связать только одной цепью, то он является деревом.
Определение. Вершина 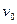 называется концевой или висячей вершиной графа
называется концевой или висячей вершиной графа 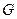 , если её степень равна единице. Ребро, инцидентное концевой вершине, также называется концевым.
, если её степень равна единице. Ребро, инцидентное концевой вершине, также называется концевым.
Если конечное дерево состоит более чем из одной вершины, оно имеет хотя бы две концевые вершины и хотя бы одно концевое ребро.
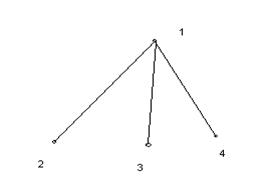
Пусть в дереве 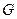 отмечена некоторая вершина
отмечена некоторая вершина 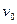 . Эту вершину называют корнем дерева
. Эту вершину называют корнем дерева 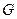 , а само дерево – деревом с корнем. В таком дереве можно естественным образом ориентировать рёбра. Любую вершину
, а само дерево – деревом с корнем. В таком дереве можно естественным образом ориентировать рёбра. Любую вершину 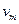 ребра
ребра 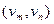 можно соединить с корнем единственной простой цепью. Если эта цепь не содержит ребра
можно соединить с корнем единственной простой цепью. Если эта цепь не содержит ребра 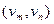 , то вводится ориентация от
, то вводится ориентация от  к
к 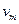 ; если цепь содержит данное ребро, то вводится ориентация от
; если цепь содержит данное ребро, то вводится ориентация от 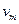 к
к  . Ориентированное таким образом дерево называется ориентированным деревом с корнем.
. Ориентированное таким образом дерево называется ориентированным деревом с корнем.
В нём все рёбра имеют направление от корня (см. рисунок 1).
Рисунок 1.
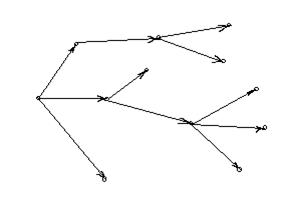
Если же изменить направления всех рёбер ориентированного дерева на противоположные (к корню), то получится ориентированный граф, который называется сетью сборки. В общем случае, такой граф тоже является ориентированным деревом. В каждую вершину ориентированного дерева, за исключением корня, входит только одно ребро. Иначе говоря, эта вершина является концом только одного ребра. Отсюда прямо следует, что в конечном дереве число вершин на один превышает число рёбер.
Замечание. Любое дерево можно ориентировать, выбрав в качестве корня любую его вершину.
Пусть дано конечное дерево 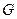 . Назовём его концевые вершины вершинами типа 1. Отметим, что если дерево имеет более двух вершин, то среди них есть неконцевые.
. Назовём его концевые вершины вершинами типа 1. Отметим, что если дерево имеет более двух вершин, то среди них есть неконцевые.
Далее удалим из дерева все вершины типа 1 и инцидентные им рёбра. Останется связный граф 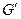 , также являющийся деревом. Дерево
, также являющийся деревом. Дерево 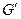 также имеет концевые вершины, которые будем называть вершинами типа 2 в дереве
также имеет концевые вершины, которые будем называть вершинами типа 2 в дереве 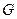 . Аналогичным образом определяются вершины типа 3 и так далее.
. Аналогичным образом определяются вершины типа 3 и так далее.
Легко видеть, что в конечном дереве имеются лишь вершины конечного числа типов, причём число вершин максимального типа равно одному или двум, так как в соответствующем дереве каждая вершина является концевой.
Теорема 16.2. Центрами дерева являются вершины максимального типа и только они.
Из данной теоремы прямо следует, что дерево имеет либо один, либо два центра. Диаметральные цепи в деревьях проходят через центр дерева, либо, если их два, через оба центра. В первом случае длина диаметральной цепи равна 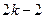 , во втором -
, во втором - 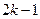 , где
, где 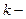 максимальный тип дерева.
максимальный тип дерева.
Определение. Цикломатическим числом конечного неориентированного графа 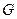 называется число, равное
называется число, равное 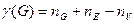 . Здесь
. Здесь 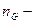 количество связных компонентов графа,
количество связных компонентов графа, 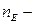 количество рёбер,
количество рёбер, 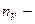 количество вершин.
количество вершин.
Цикломатическое число дерева равно нулю. Цикломатические числа остальных конечных графов положительны.
- Ориентированные графы.
Понятие ориентированного графа (орграфа) было определено ранее. Сейчас рассмотрим подробнее, как выглядят в таком графе пути и циклы.
Пусть дан ориентированный граф 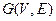 . Каждое ребро имеет начало
. Каждое ребро имеет начало 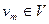 и конец
и конец 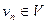 ; также говорят, что данное ребро выходит из вершины
; также говорят, что данное ребро выходит из вершины 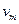 и входит в вершину
и входит в вершину  .
.
Дадим определение пути в ориентированном графе. Сразу оговоримся, что это понятие можно определять различными способами; мы приводим только один.
Определение. Путь из вершин и рёбер – это такая последовательность рёбер и вершин графа 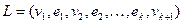 , в которой вершина
, в которой вершина 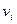 является началом
является началом 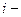 го ребра, а вершина
го ребра, а вершина 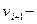 его концом. Вершина
его концом. Вершина 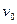 называется началом пути
называется началом пути 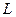 , вершина
, вершина 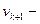 его концом, число рёбер
его концом, число рёбер 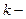 длиной пути.
длиной пути.
Путь, состоящий из одной вершины, имеет нулевую длину. Каждому пути 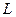 ненулевой длины взаимно однозначно соответствует последовательность
ненулевой длины взаимно однозначно соответствует последовательность 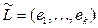 рёбер этого пути. Её называют путём из рёбер. Такое понятие пути – аналог соответствующего понятия для неориентированного графа. Наконец, для графа, не содержащего кратных рёбер, можно указать взаимнооднозначное соответствие с последовательностью
рёбер этого пути. Её называют путём из рёбер. Такое понятие пути – аналог соответствующего понятия для неориентированного графа. Наконец, для графа, не содержащего кратных рёбер, можно указать взаимнооднозначное соответствие с последовательностью 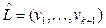 вершин пути. В зависимости от ситуации удобнее использовать тот или иной способ обозначения пути.
вершин пути. В зависимости от ситуации удобнее использовать тот или иной способ обозначения пути.
Определение. Путь 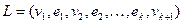 называется ориентированным циклом, если состоит более, чем из одного элемента, и его начало совпадает с его концом.
называется ориентированным циклом, если состоит более, чем из одного элемента, и его начало совпадает с его концом.
Начало цикла обычно не фиксируется, иначе говоря, все пути, получающиеся друг из друга циклическими сдвигами – это один и тот же цикл. Определение простого ориентированного цикла аналогично соответствующему определению для неориентированного цикла – это цикл, в котором каждая вершина инцидентна ровно двум его рёбрам. Любой граф, содержащий циклы, можно “укоротить” до простого. Граф, не содержащий циклов, называется ациклическим.
Определение. Вершина ориентированного графа называется начальной, если в неё ни входит ни одно ребро и конечной, если из неё не выходит ни одно ребро.
Во всяком ациклическом графе есть хотя бы одна начальная и хотя бы одна конечная вершина. Максимальным рангом 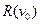 вершины ориентированного графа называется максимальная из длин путей этого графа с концом в вершине
вершины ориентированного графа называется максимальная из длин путей этого графа с концом в вершине 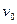 . Ранг вершины равен нулю тогда и только тогда, когда вершина является начальной. Если же через вершину проходит какой-нибудь цикл, то
. Ранг вершины равен нулю тогда и только тогда, когда вершина является начальной. Если же через вершину проходит какой-нибудь цикл, то  .
.
Пусть вершины конечного ориентированного графа пронумерованы от 1 до 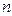 . Нумерация вершин называется правильной на ребре
. Нумерация вершин называется правильной на ребре 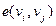 , если
, если 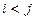 и правильной на графе
и правильной на графе 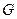 , если она правильна на всех его рёбрах. Правильная нумерация вершин графа возможна только в том случае, если он ациклический.
, если она правильна на всех его рёбрах. Правильная нумерация вершин графа возможна только в том случае, если он ациклический.
Понятия длины путей, протяжённости и расстояния между вершинами определяются для ориентированного графа так же, как для неориентированного графа.
- Графы с помеченными вершинами и рёбрами.
Нередко приходится иметь дело с различиями между вершинами графа. Тогда их разбивают на классы. Каждый класс состоит из вершин, имеющих обще свойство. Примером таких свойств могут быть следующие из уже описанных ранее свойств: иметь данную степень, иметь данное расстояние от корня, иметь данный ранг и так далее. В других случаях разбиение определяется свойствами объектов, описываемых при помощи графа. Например, структурная формула химического соединения – это граф, в котором вершины соответствуют атомам, рёбра – валентным связям, а классы состоят из вершин, соответствующих атомам одного и того же элемента.
Пусть дано разбиение графа на классы (всё равно, по какому признаку). Каждой вершине можно соотнести метку, указывающую, какому именно классу она принадлежит. Такая вершина называется помеченной. Метки являются элементами заданно множества. Иногда они явно указывают на свойства, определяющие классы: например, степени, ранги вершин, и их расстояния от корня можно метить соответствующими числами. Однако часто абстрагируются от конкретного характера отличий между вершинами, и тогда метки указывают только на сам факт сходства вершин или их различия. Соотнесение таких меток вершинам называют раскраской их в разные цвета. Аналогичным образом говорят о раскраске рёбер графа и вообще о раскраске элементов произвольного множества.
Дата добавления: 2015-08-11; просмотров: 3050;
