Комплексное сопротивление
Введение комплексного представления токов и напряжений требует определить и сопротивление элементов электрических цепей в комплексной форме - Z.
Хорошо известно, что сопротивление резистора определяется как отношение напряжения на резисторе к току, протекающему через него. Если напряжение и ток представлены в комплексной форме, то:
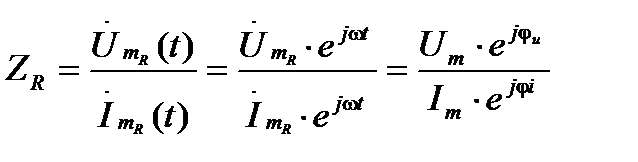
Но в предыдущей лекции было установлено, что 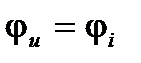 . Поэтому:
. Поэтому:
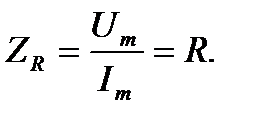 (4.1)
(4.1)
Таким образом, видим, что комплексное сопротивление резистора выражается только действительным числом. Оно не вносит фазовых искажений между током и напряжением. Чтобы подчеркнуть этот факт такое сопротивление часто называют активным.
Комплексное сопротивление емкости определяется отношением:
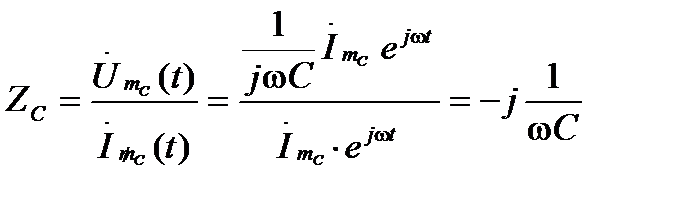 . (4.2)
. (4.2)
Видим, что комплексное сопротивление емкости переменному току выражается мнимым числом. Мнимая единица -j физически определяет сдвиг фаз между током и напряжением на 90о. Это хорошо согласуется с ее математическим значением:
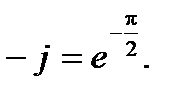
Поэтому на емкости напряжение отстает от тока на 90о. Это означает, что сначала растет ток, протекающий через конденсатор, затем, с некоторым отставанием увеличивается заряд и напряжение.
Коэффициент 1/ 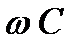 определяет величину сопротивления в Омах. Он обратно пропорционален частоте, называется емкостным сопротивлением и обозначается ХС, т.е.:
определяет величину сопротивления в Омах. Он обратно пропорционален частоте, называется емкостным сопротивлением и обозначается ХС, т.е.:
 . (4.3)
. (4.3)
Комплексное сопротивление индуктивности определяется отношением:
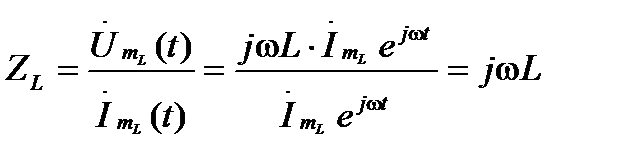 . (4.4)
. (4.4)
И в этом случае сопротивление выражается мнимым числом. Но так как это число положительное, то это означает, что на индуктивности напряжение опережает ток на 90о.
Коэффициент wL определяет величину сопротивления в Омах.
Он пропорционален частоте, называется индуктивным сопротивлением и обозначается ХL, т.е.:
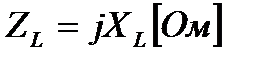 . (4.5)
. (4.5)
Чтобы подчеркнуть тот факт, что сопротивления емкости и индуктивности выражаются мнимыми числами, их называют реактивными сопротивлениями, а конденсатор и индуктивность - реактивными элементами цепи.
Определим теперь комплексное сопротивление электрической цепи, содержащей активные и реактивные элементы, например последовательно включенные R, L и С элементы (рис.3.1). Такая цепь представляет замкнутый  контур, поэтому для нее справедлив второй закон Кирхгофа:
контур, поэтому для нее справедлив второй закон Кирхгофа:
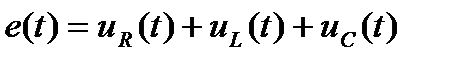 . (4.6)
. (4.6)
В последнем выражении проведем замену символов мгновенных напряжений и ЭДС на их комплексные изображения по правилам, определенным в лекции 2, 3. Такой прием получил название символического метода. Так как ток, протекающий через все элементы последовательной цепи одинаков, то (3.6) приходит к виду:
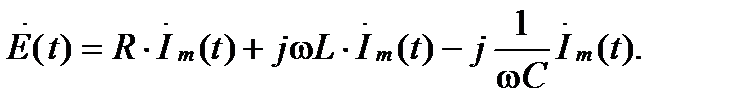
Преобразуем это выражение к виду:
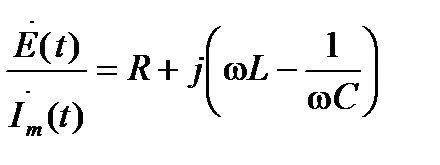 .
.
По определению выражение в правой части последнего равенства есть не что иное, как комплексное сопротивление цепи рис.3.1, т.е.:
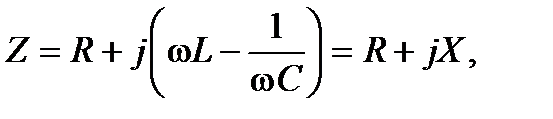 (4.7)
(4.7)
где R - действительная часть или активное сопротивление цепи.
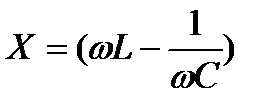 - мнимая часть или реактивное сопротивление цепи.
- мнимая часть или реактивное сопротивление цепи.
Выражение (.7) представляет комплексное сопротивление в алгебраической форме. Соотношения между составляющими комплексного сопротивления находятся в полном соответствии с соотношениями для комплексного представления тока. Но для большей наглядности вводится
понятие треугольника сопротивления (рис.3.2).
| X |
| Z |
| R |
| Рис. 3.2 |
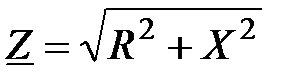 . (4.8)
. (4.8)
| Z |
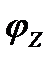 катет – активным сопротивлением цепи R, причем:
катет – активным сопротивлением цепи R, причем:
 (4.9)
(4.9)
Противолежащий катет - реактивным сопротивлением Х, причем:
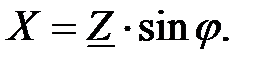 (4.10)
(4.10)
Угол 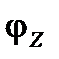 определяет сдвиг фаз между током и напряжением, который вносится комплексным сопротивлением цепи, причем:
определяет сдвиг фаз между током и напряжением, который вносится комплексным сопротивлением цепи, причем:
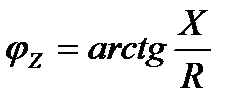 . (4.11)
. (4.11)
Учитывая выражения (4.8) ¸ (4.11), легко перейти от алгебраической к тригонометрической форме комплексного сопротивления:
Z =Z 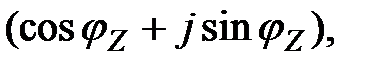 (4.12)
(4.12)
a применив формулу Эйлера получить показательную форму:
Z =Z 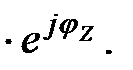 (4.13)
(4.13)
Теперь можно записать закон Ома для участка цепи без источника ЭДС в комплексном изображении:
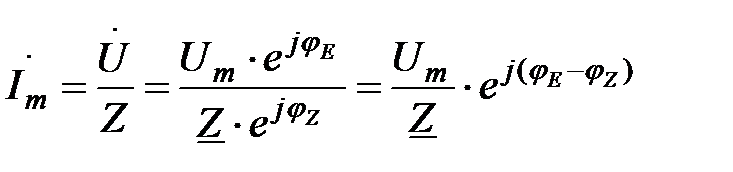 (4.14)
(4.14)
Выражение (4.14) показывает, что в цепях переменного тока модуль тока определяется отношением модуля напряжения (его амплитудного значения) к модулю комплексного сопротивления, а фаза тока определяется разностью фаз напряжения и комплексного сопротивления. Отсюда вытекает еще одно полезное для практики выражение:
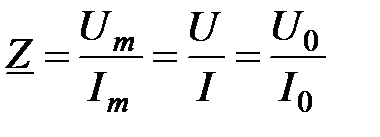 . (4.15)
. (4.15)
Дата добавления: 2015-08-11; просмотров: 2200;
