Правила Кирхгофа.
1) Сумма токов, направленных к точке разветвления, равна сумме токов, направленных от нее.
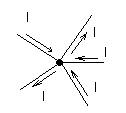 I1+I3+I5=I2+I4
I1+I3+I5=I2+I4
Преобразуя это соотношение, получим:
I1+(-I2)+I3+(-I4)+I5=0
Т.е. 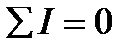 алгебраическая сумма токов в точке разветвления равна нулю.
алгебраическая сумма токов в точке разветвления равна нулю.
При этом токи, направленные к узлу, считаются положительными, а токи, направленные от узла – отрицательными (или наоборот).
Узлом называют точку цепи из которой провода уходят больше чем в двух направлениях
2) В замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжения в отдельных сопротивлениях.
При этом положительными надо считать ЭДС, направления которых совпадают с произвольно выбранным направлением обхода по контуру.
Если контур не содержит источников, то 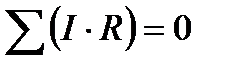 .
.
1. Пример: Решение задачи методом непосредственного применения законов Кирхгофа.
Дано:
Е1=30 В; Е2=20 В; Е3=15 В.
R1=4 Ом; R2=2 Ом; R3=1 Ом; R4=10 Ом; R5=6 Ом; R6=3 Ом.
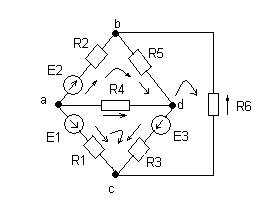 Решение:
Решение:
1-е правило – число узловых уравнений должно быть на единицу меньше числа узлов электрической цепи.
2-е правило – недостающие уравнения составляются по второму Кирхгофа; при этом нужно выбирать наиболее простые контуры (с меньшим числом источников ЭДС и сопротивлений) в таком порядке, чтобы в каждом новом контуре содержалась, по меньшей мере, одна ветвь, не входившая в контуры, для которых уже составлены уравнения.
1.Составим уравнения по первому закону Кирхгофа, т.к. в схеме четыре узла, то можем составить (4-1)=3 уравнения.
Узел «а» -I2 - I1 - I4 = 0
Узел «в» I2 + I6 - I5 = 0
Узел «с» I1 + I3 - I6 = 0
2. Составляем недостающие уравнения по второму закону Кирхгофа (для решения системы с 6-ю неизвестными необходимо 6 уравнений).
Контур «aвda» : I2R2 + I5R5 – I4R4 = E2
Контур «adca» : I4R4 + I3R3 – I1R1 = E3 – E1
Контур «abR6ca» : I2R2 – I6R6 – I1R1 = E2 – E1
Подставив значения E и R, получим систему уравнений:



- I2 – I1- I4 = 0
I2 + I6 – I5 = 0
I1 + I3 – I6 = 0
2I2 + 6I5 – 10I4 = 20
10I4 + I3 – 4I1 = 15 – 30
2I2 – 3I6 – 4I1 = 20 – 30
Далее решаем полученную систему уравнений любым возможным способом (можно на ЭВМ).
Решив систему уравнений, получим:
I1 = 1.18 A; I2 = - 0.1 A; I3 = 0.5 A; I4 = -1 A; I5 = 1.57 A; I6 = 1.68 A.
Решение системы уравнений, для сложной цепи, требует значительной затраты времени, поэтому можно использовать более простые методы.
2. Метод контурных токов.
Метод контурных токов исходит из того, что в каждом контуре течет свой контурный ток.
Ik1 (R2 + R5 + R4) – Ik2 R4 – Ik3 R5 = E2
Ik2 (R4 + R3 + R1) – Ik1 R4 – Ik3 R3 = E3 – E1
Ik3 (R6 + R3 + R5) – Ik1 R5 – Ik2 R3 = - E3
Подставив значения, получим систему уравнений:
Ik1 (2 + 6 + 10) – Ik2 10 – Ik3 6 = 20
Ik2 (10 + 1 + 4) – Ik1 10 – Ik3 1 = 15 – 30
Ik3 (3 + 1+ 6) – Ik1 6 – Ik2 1 = - 15
18Ik1 – 10Ik2 – 6Ik3 = 20
15Ik2 – 10Ik1 – Ik3 = - 15
10Ik3 – 6Ik1 – Ik2 = -15
Решив систему уравнений, получим:
Ik1 = - 0.1 A; Ik2 = - 1.18 A; Ik3 = - 1.68 A
Чтобы проверить правильность расчета нужно составить баланс мощности, т.е. мощность источника должна быть равна мощности потребителя:
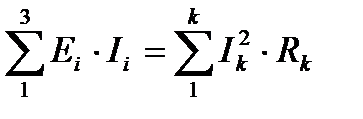
Е1 I1 + E2 I2 + E3 I3 = I12 R1 + I22 R2 + I32 R3 + I42 R4 + I52 R5 + I62 R6
30 1.18 – 20 0.1 + 15 0.5 = 40.9 Вт
1,182 4 + 0,12 2 + 0,52 1 + 12 10 + 1,572 6 + 1,682 3 = 39,1 Вт
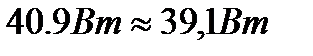 (баланс сходится)
(баланс сходится)
Если ток и напряжение совпадают, то работает в режиме генератора, то мощность со знаком «+»
Если ток и напряжение встречны, то работает в режиме потребителя, то мощность со знаком «-».
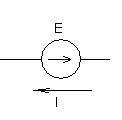
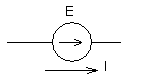
« + » « – »
Дата добавления: 2015-08-11; просмотров: 1001;
