Анализ изменения давления в цилиндре насоса в период всасывания
Рассмотрим процесс всасывания одноцилиндрового приводного насоса одинарного действия, который откачивает жидкость из приемного резервуара открытого типа. Давление на поверхности жидкости постоянно и равно ро, ось цилиндра насоса, расположенного горизонтально, находится на высоте zв от свободной поверхности перекачиваемой жидкости плотностью ρ.

Рис. 10. Схема одноцилиндрового насоса одинарного действия.
Запишем уравнение Бернулли для двух сечений 1–1 и 2–2, приняв за плоскость сравнения сечение 1–1:

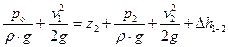 , (18)
, (18)
где v1 – скорость перемещения поверхности жидкости в сечении 1–1; z2=zв – вертикальное расстояние между сечением 1–1 и центром тяжести сечения 2–2, совпадающего с поверхностью поршня, контактирующей с жидкостью; p2=pц – давление жидкости в цилиндре насоса в период всасывания; v2=vп – скорость движения жидкости в цилиндре, равная скорости поршня; 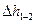 – потери энергии на перемещение жидкости между рассматриваемыми сечениями.
– потери энергии на перемещение жидкости между рассматриваемыми сечениями.
При круговой циркуляции жидкости (характерной для ряда операций, выполняемых на скважинах) поверхность жидкости в приемном резервуаре практически неподвижна и v1=0.
Решая уравнение (18) относительно напора в цилиндре 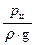 с учетом высказанных замечаний, получим:
с учетом высказанных замечаний, получим:
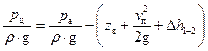 . (19)
. (19)
Потери энергии 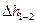 между сечениями 1-1 и 2-2 состоят из потерь в местных сопротивлениях
между сечениями 1-1 и 2-2 состоят из потерь в местных сопротивлениях 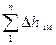 всасывающего трубопровода, потерь по длине
всасывающего трубопровода, потерь по длине 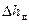 и потерь на преодоление сил инерции в цилиндре
и потерь на преодоление сил инерции в цилиндре  и в трубопроводе
и в трубопроводе 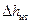 :
:
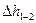 =
= 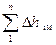 +
+ 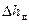 +
+  +
+ 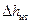 . (20)
. (20)
Установлено, что потери в клапане изменяются особым образом в сравнении с другими местными сопротивлениями, поэтому выделим эти потери в виде отдельного слагаемого. Тогда местные потери представим в виде:
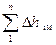 =
= 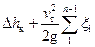 , (21)
, (21)
где 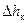 – потери напора во всасывающем клапане;
– потери напора во всасывающем клапане; 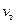 – скорость движения жидкости во всасывающем трубопроводе;
– скорость движения жидкости во всасывающем трубопроводе; 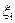 – коэффициент местных потерь i-го местного сопротивления всасывающего трубопровода.
– коэффициент местных потерь i-го местного сопротивления всасывающего трубопровода.
Выражая в уравнении (21) скорость движения жидкости в трубопроводе через скорость поршня, получим:
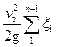 =
= 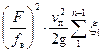 , (22)
, (22)
где 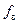 – площадь поперечного сечения всасывающего трубопровода.
– площадь поперечного сечения всасывающего трубопровода.
Потери напора по длине 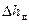 всасывающего трубопровода (в уравнении 20) представим по известной формуле Дарси-Вейсбаха:
всасывающего трубопровода (в уравнении 20) представим по известной формуле Дарси-Вейсбаха:
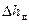 =
= 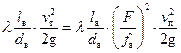 , (23)
, (23)
где λ – коэффициент гидравлического трения; lв – длина всасывающего трубопровода; dв – внутренний диаметр всасывающего трубопровода.
С учетом отмеченных замечаний и обозначений, уравнение (19) примет вид:
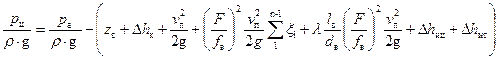 . (24)
. (24)
Объединим потери в местных сопротивлениях с потерями по длине:
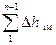 +
+ 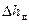 =
= 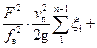

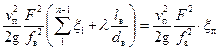 , (25)
, (25)
где 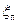 – приведенный коэффициент гидравлических сопротивлений всасывающего трубопровода.
– приведенный коэффициент гидравлических сопротивлений всасывающего трубопровода.
Подставив в уравнение (25) скорость движения поршня по уравнению (9), без учета влияния длины шатуна, получим:
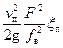
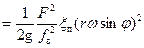 . (26)
. (26)
Потери напора на преодоление сил инерции жидкости в цилиндре вычислим по формуле:

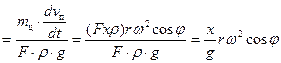 , (27)
, (27)
где mц – масса жидкости в цилиндре.
Аналогично вычислим потери напора на преодоление сил инерции жидкости в трубопроводе:
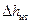
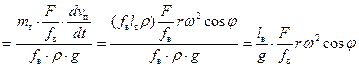 , (28)
, (28)
где mт – масса жидкости во всасывающем трубопроводе.
Для исключения из уравнений (26), (27) и (28) тригонометрических функций, воспользуемся уравнением (8) из которого выразим cosφ, а затем – sinφ:
cosφ 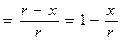 . (29)
. (29)
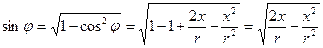 . (30)
. (30)
Подставив выражение (30) в уравнения (26), а (29)– в уравнения (27) и (28), получим:
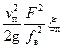 =
= 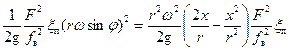 . (31)
. (31)
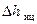
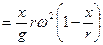 . (32)
. (32)
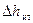
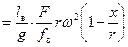 . (33)
. (33)
Кроме того, преобразуем в уравнении (24) выражение для скоростного напора к виду:
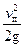
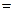
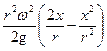 . (34)
. (34)
Подставив выражения (31) – (34) в уравнение (24) и выполнив некоторые преобразования, получим:

 (35)
(35)
Умножив правую и левую части уравнения (35) на (ρ∙g) получим зависимость давления в цилиндре насоса от величины х перемещения поршня:
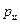
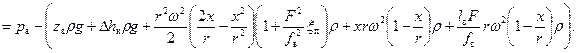 (36)
(36)
Анализ уравнения (36) показывает, минимальное давление в цилиндре насоса будет в начале процесса всасывания (при х=0), а максимальное – в конце (при х=2r). Тогда, уравнение (36) соответственно примет вид:
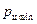
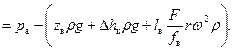 (37)
(37)

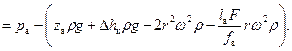 (38)
(38)
Дата добавления: 2015-07-10; просмотров: 1674;
