Средняя квадратическая ошибка функции измеренных величин

а) Функция общего вида:

.

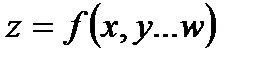Пусть аргументы измерены с ошибками ∆x₁, ∆x₂,…; ∆y₁, ∆y₂,…; ∆w₁, ∆w₂…

Тогда

.

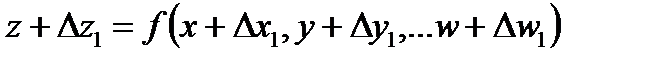Так как ошибки ∆x, ∆y, ∆w малы, то функцию можно разложить в ряд Тейлора, ограничившись членами первой степени:

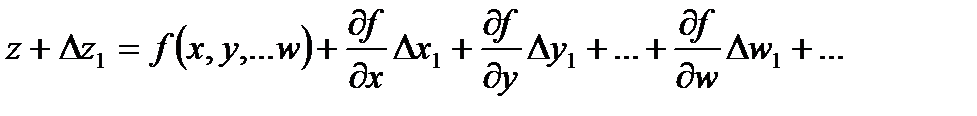
Отсюда составим систему уравнений случайных ошибок:

.

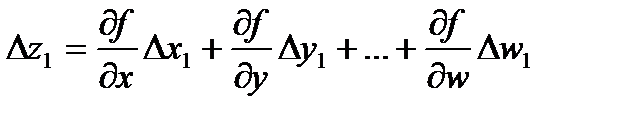Но ∆x, ∆y…имеют бесконечное число измерений каждая и характеризуются средними квадратическими ошибками. Поэтому можно составить бесконечное число уравнений, аналогичных выше приведенному:

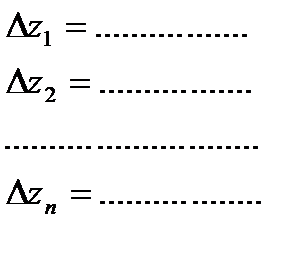Возведем равенства в квадрат, сложим и разделим на n.

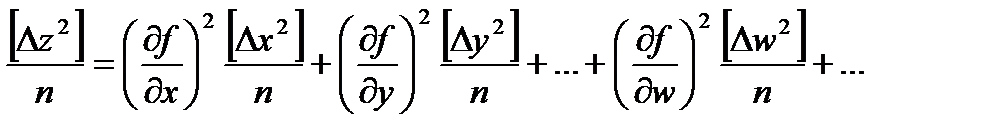
0 n→∞.

Отсюда

→ .

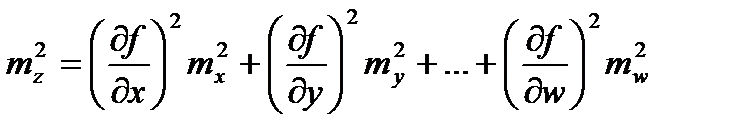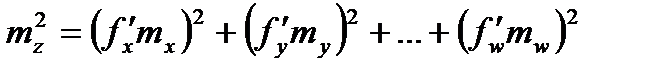Квадрат средней квадратической ошибки функции общего вида равен сумме квадратов произведений частных производных по каждому аргументу на средние квадратические ошибки соответствующих аргументов.

б) Функция вида z=x+y (суммы), m_z=?

Дано: х – измерено несколько раз с ошибками ∆х₁; ∆х₂,… ∆х_n

у – измерено несколько раз с ошибками ∆у₁, ∆у₂,… ∆у_n

z – будет вычислено несколько раз с ошибками ∆z₁, ∆z₂,… ∆z_n.

;

.

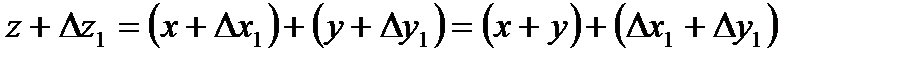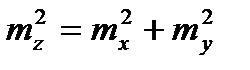Эта же формула справедлива для функции вида z=x-y, так как после выше приведенных рассуждений перед последним членом будет знак (-). Но он все равно стремится к нулю.

Поэтому можно сделать вывод, что квадрат средней квадратической ошибки алгебраической суммы двух аргументов равен сумме квадратов средних квадратических ошибок слагаемых.

Если m_х=m_у=m, то m_z=± .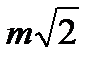

Пусть 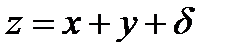, перепишем 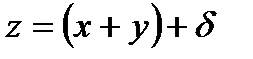. Тогда можно записать:

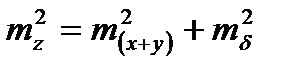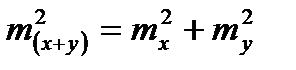, но , поэтому

.

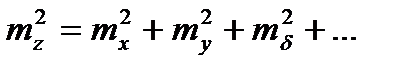Если 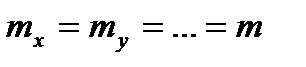, то при n слагаемых 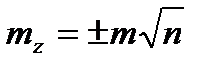, то есть квадрат средней квадратической ошибки суммы аргументов равен сумме квадратов средних квадратических ошибок слагаемых.

Средняя квадратическая ошибка алгебраической суммы измеренных с одинаковой точностью величин в 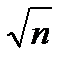раз больше средней квадратической ошибки одного слагаемого.

в) Функция вида 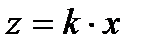(произведения).

k – постоянное число безошибочное.

х – измерено несколько раз с ошибками ∆х₁, ∆х₂,… ∆х_n.

z – будет вычислено несколько раз с ошибками ∆z₁, ∆z₂,…, ∆z_n.

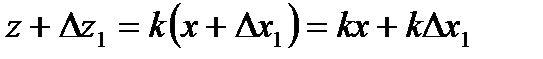
отсюда 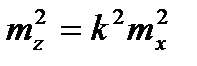или ,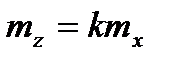

то есть средняя квадратическая ошибка произведения постоянного числа на аргумент равна произведению постоянного числа на среднюю квадратическую ошибку аргумента (измеряемой величины).