Арифметическая середина и ее свойства
Пусть ℓ1, ℓ2,… ℓn – ряд измерений некоторой величины Х. За наилучшее приближение к значению неизвестной величины принимают арифметическую середину ℓ0, то есть среднее арифметическое значение:
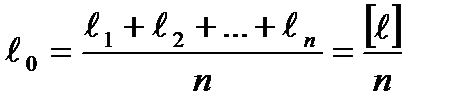 .
.
Арифметическая середина обладает рядом свойств, из которых можно выделить следующие:
1-е свойство: при неограниченном увеличении числа измерений n арифметическая середина ℓ0 стремится к истинному значению Х, то есть является наиболее вероятнейшим значением измеряемой величины.
+ 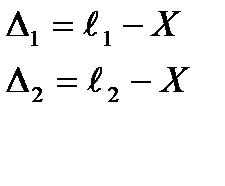 просуммируем уравнения и разделим на n
просуммируем уравнения и разделим на n
..................
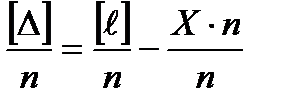 │ 0=ℓ0-Х.
│ 0=ℓ0-Х.
↓ 0 по свойству компенсации.
Поэтому 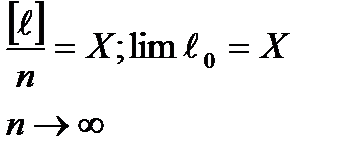 ,
, 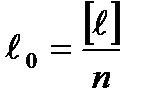 .
.
2-е свойство: сумма отклонений δi измеренных значений ℓi от арифметической середины ℓ0 тождественно равна нулю.
+ 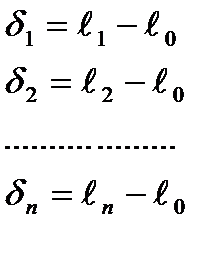 Это вероятнейшие случайные ошибки.
Это вероятнейшие случайные ошибки.
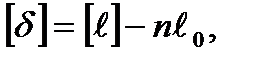 но
но 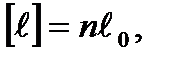 поэтому
поэтому 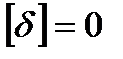 .
.
3-е свойство: средняя квадратическая ошибка М арифметической середины в 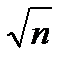 раз меньше средней квадратической ошибки результата отдельного измерения m.
раз меньше средней квадратической ошибки результата отдельного измерения m.
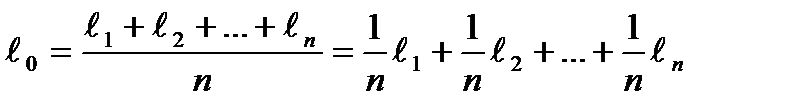 .
.
Рассматривая эту формулу как функцию общего вида, найдем:
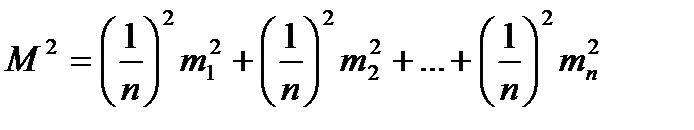 .
.
Так как измерения равноточные и
то 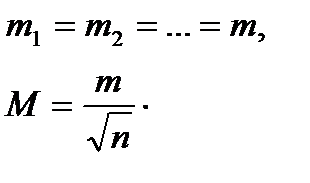
Дата добавления: 2015-08-11; просмотров: 2744;
