Оценка точности ряда измерений по вероятнейшим ошибкам
Истинные случайные ошибки ∆ обычно остаются неизвестны. Поэтому для оценки точности используют вероятнейшие ошибки, то есть отклонения отдельных результатов измерений от арифметической середины.
Составим уравнения истинных и вероятнейших случайных ошибок:
Ур-я ист. сл. ош. Ур-я вероятн. сл. ош.
▬ 
,
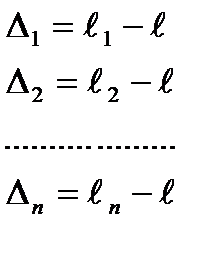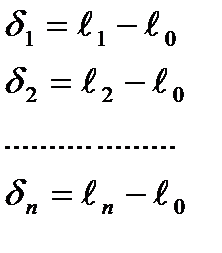и
где ℓi – измеренные значения; ℓ – истинное значение измеренной величины; ℓ0 – арифметическая середина.
Из первой системы вычтем вторую:
,
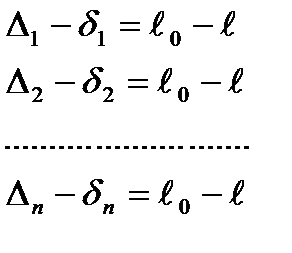
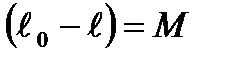где М представляет собой случайную ошибку арифметической середины.
Перепишем равенства:
2
+ 
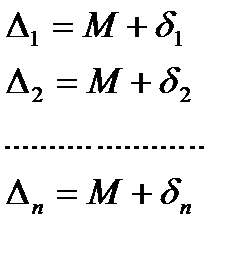Возведем равенства в квадрат и сложим их;
||
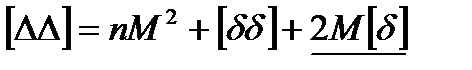
0 по второму свойству арифметической середины.
Разделив на n полученное равенство, имеем:
.
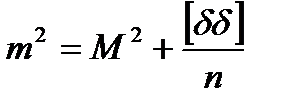Учтем, что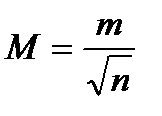 
. Тогда формула Бесселя:
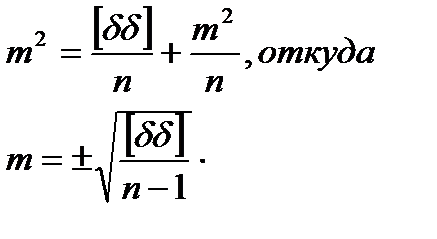
Дата добавления: 2015-08-11; просмотров: 1108;