Средняя квадратическая, предельная и относительная ошибки

Для суждения о степени точности ряда измерений нужно иметь среднее значение ошибки. Среднее арифметическое из измерений нельзя брать, так как из-за разных знаков ряд с отдельными крупными ошибками может оказаться точнее ряда с меньшими ошибками:

25,5; 24,5; 25,0 – m_ср.=0 Х=25м.

25,04; 24,97; 25,04 – m_ср.=0,02 м

Если взять ошибки по абсолютной величине, то два ряда измерений с одинаковыми по абсолютной величине средними ошибками могут быть

ошибочно приняты равноточными и наличие крупных ошибок не будет отражено:

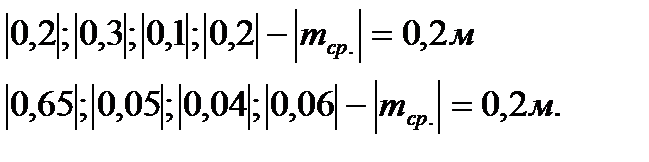
Поэтому в качестве критерия для оценки точности ряда измерений используют не зависящую от знаков отдельных ошибок и рельефно показывающую наличие крупных ошибок среднюю квадратическую ошибку. Квадрат этой ошибки принимают равным среднему арифметическому из квадратов отдельных случайных ошибок, то есть:

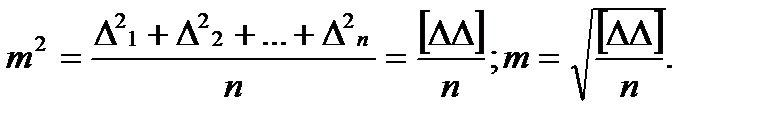– формула Гаусса, где Δ – истинная ошибка измерения.

По теории вероятностей подсчитано, что при большом количестве измерений случайная ошибка одного измерения превосходит m.

∆>1m – в 32 случаях из 100 измерений.

∆>2m – в 5 случаях из 100 измерений.

∆>3m – в 3 случаях из 1000 измерений.

Поэтому утроенную среднюю квадратическую ошибку считают предельной

∆_lim=3m.

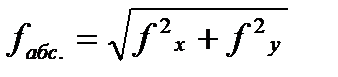Часто точность произведенных измерений лучше оценивается относительной ошибкой, то есть отношением абсолютной ошибки к измеряемой величине, выражаемой правильной дробью с числителем, равным 1. Эта ошибка характеризует в основном линейные измерения и измерения площади участков. Например, в замкнутом полигоне теодолитного хода линейные измерения оцениваются относительной ошибкой ; где – абсолютная ошибка, Р – периметр полигона.