Прямая и обратная геодезические задачи

Прямая геодезическая задача заключается в том, что по известным координатам одной точки, дирекционному углу и расстоянию до другой определяют координаты последней. При вычислениях чаще всего дирекционные углы переводят в румбы. Прямая геодезическая задача решается и при вычислении координат вершин полигонов.

Дано: х₁; у₁ – координаты начальной точки; α_1-2; α_2-3; α_3-4; α_4-5; α_5-1 – дирекционные углы сторон полигона. d_1-2; d_2-3………………..d_5-1 – горизонтальные проложения сторон полигона. Найти: х₂ и у₂; х₃ и у₃…………..х₅ и у₅. Разница между координатами соседних точек называется приращением координат: х₂ – х₁=Δх_1-2; у₂ – у₁=Δу_1-2. Отсюда х₂=х₁+Δх_1-2; у₂=у₁+Δу_1-2. Из треугольника следует (рис. 12): Δх_1-2=d_1-2∙cosr_1-2; Δу_1-2= d_1-2∙sinr_1-2.

Из рис. 13 следует: х₃=х₂+Δх_2-3; у₃=у₂+Δу_2-3; Δх_2-3=d_2-3∙cosr_2-3;

Δу_2-3= d_2-3∙ sinr_2-3.

Перейдем к общему случаю: х_n=х_n-1+Δх_n; у_n =у_n-1+Δу_n; Δх_n= d_n∙cosr_n; Δу_n= d_n sinr_n.

При вычислениях учитываются знаки приращений координат в зависимости от четверти, в которую направлена линия (см. выше). Если вместо румбов использовать дирекционные углы, то знаки перед приращениями координат получаются сами собой.

Х

2

3

1 Δх_1-2 1

х₂

х₁

Δу_1-2

4 у₂ У

5 у₁

Рис. 12. Решение прямой геодезической задачи для линии 1-2

Х

2

Δх_2-3

3

х₃

Δу_2-3

х₂

У

у₂ у₃

Рис. 13. Решение прямой геодезической задачи для линии 2-3

Координаты n – ой точки полигона можно выразить и через координаты первой точки:

х₂=х₁+Δх_1-2;

х₃=х₂+Δх_2-3=х₁+ (Δх_1-2+ Δх_2-3);

х₄=х₃+Δх_3-4= х₁+ (Δх_1-2+ Δх_2-3+ Δх_3-4);

х₅=х₄+Δх_4-5= х₁+ (Δх_1-2+ Δх_2-3+ Δх_3-4+Δх_4-5);

…… х_n= х₁+ 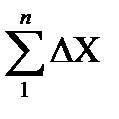и у_n=у₁+ .

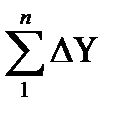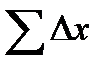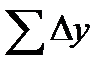и – суммы приращений координат.

Отсюда запишем:

х_n - х₁=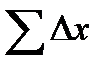

у_n - у₁=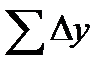

В случае замкнутого полигона, когда, обойдя все вершины поочередно, мы возвращаемся в исходную, х_n - х₁=0 и у_n – у₁=0. Следовательно, для замкнутого полигона сумма приращений координат по обеим осям равна нулю.

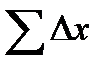_теор.=0 и 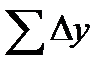_теор.=0.

Однако в связи с ошибками в угловых и линейных величинах эта сумма будет несколько отличаться от 0. Мы возвратимся не в точку 1, а в 1΄

(рис. 14).

Полученная разница в суммах приращений координат называется невязкой:

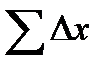_изм.=f_х≠0 – невязка по х;

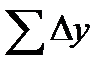_изм.=f_у ≠0 – невязка по у.

Для оценки точности полигона вычисляют абсолютную невязку:

(1 - 1΄)=f_абс.= ,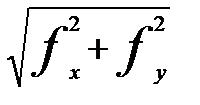

а затем относительную ошибку:

f_отн.= 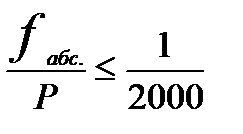; Р – периметр.

Х 2

f_у

1

f_абс. f_х 3

1'

5 4

У

Рис. 14. Виды невязок в полигоне

Если условие неравенства выполняется, полученную невязку по осям координат распределяют в вычисленные приращения в виде поправок с обратным невязке знаком, пропорционально значениям горизонтальных проложений: большую поправку в большее значение проложения.

Обратная геодезическая задача заключается в вычислении дирекционного угла и горизонтального проложения линии, по известным координатам ее начальной и конечной точек. Из предыдущих рисунков видно, что

d= 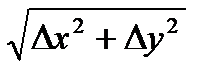; tgr= 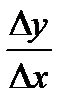; r=arctgr; d= = .

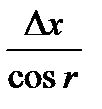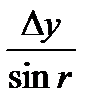Дирекционный угол находят по полученному румбу, учитывая четверть, в которую направлена прямая. Четверть определяется по знакам приращений координат:

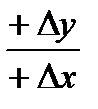1 четверть α=r; 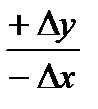2 четверть α=180° - r;

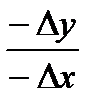3 четверть α=r+180°; 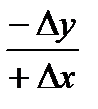4 четверть α=360° - r.

6.Топографические карты и планы

Понятие о плане, карте, профиле

План есть уменьшенное и подобное изображение на бумаге горизонтальной проекции сравнительно небольшого участка местности. Размеры участка до

25 км². В этом случае не учитывается кривизна Земли. Степень уменьшения изображения сравнительно небольшая: 100, 200, 500…5000раз. Для удобства пользования на планах наносится координатная сетка. Планы могут быть горизонтальными (контурными), высотными и контурно-высотными (топографическими).

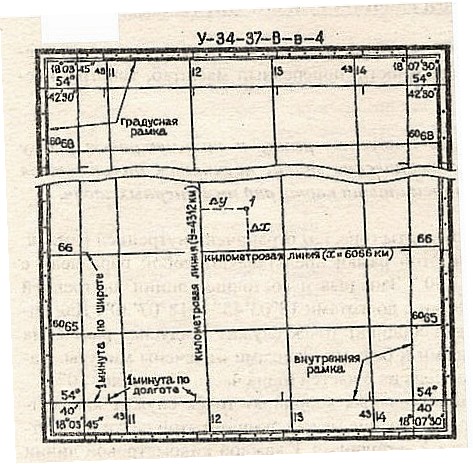
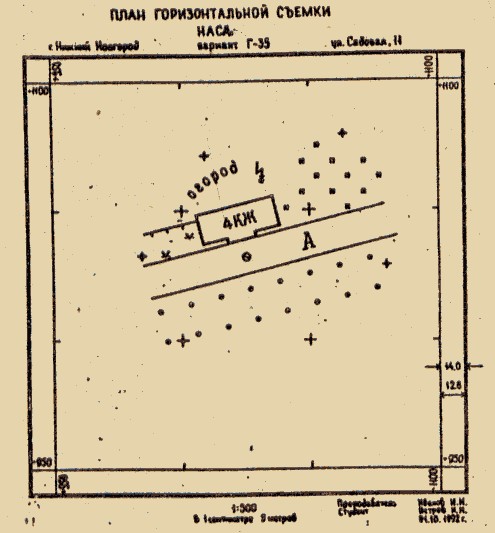
координатная сетка километровая сетка

План М 1:1000 Карта М 1:10000

Рис. 15. План, карта

Карта – уменьшенное и закономерно искаженное вследствие влияния кривизны Земли изображение на бумаге горизонтальной проекции значительной части или всей земной поверхности. Степень уменьшения больше по сравнению с планом: 10000 раз, 50000….. . Искажения происходят из-за невозможности развертывания сферических поверхностей (геоид, эллипсоид) в плоскость (бумага плоская) без разрывов и складок. На картах наносят градусные и километровые сетки. Все карты контурно – высотные (топографические).

По планам и картам можно решать ряд задач:

1. Определение расстояний между точками.

2. Определение прямоугольных и географических координат точек.

3. Определение абсолютных отметок точек.

4. Ориентирование линий местности.

5. Построение профилей по заданным направлениям.

6. Определение крутизны ската.

7. Определение водосборной площади и другие.

Порядок решения задач смотри [5].

Профиль местности есть линия пересечения земной поверхности с отвесной (вертикальной) плоскостью, расположенной в заданном направлении (PQ) (рис. 16). Его уменьшенное изображение на бумаге также называется профилем. Направление сечения может быть прямолинейным, ломаным или криволинейным.

Р

Q

Рис. 16. Профиль