Закон распределения Вейбулла
Для распределения Вейбулла плотность распределения времени безотказной работы Т изделия имеет вид
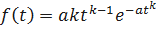 ;
;
здесь aи k– параметры закона распределения Вейбулла.
Определим q(t). Имеем
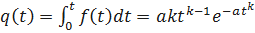 .
.
Введём новую переменную x вида
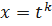 ;
; 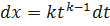 ;
;
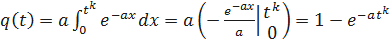 ;
; 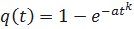
Определим P(t). Имеем
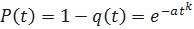 ;
; 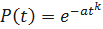
Определим 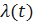 . Получим
. Получим
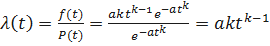 .
.
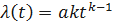 .
.
Определим среднее время безотказной работы. Имеем
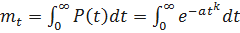 .
.
Введём новую переменную uвида
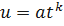 ;
; 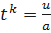 ;
; 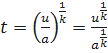 ;
;
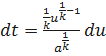 ;
; 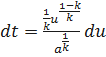 ;
;
если 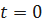 ,то
,то 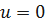 .
.
если 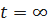 ,то
,то 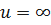 .
.
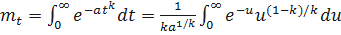 .
.
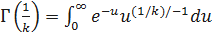 – гамма-функция
– гамма-функция
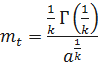
Определим дисперсию времени безотказной работы T.
Имеем
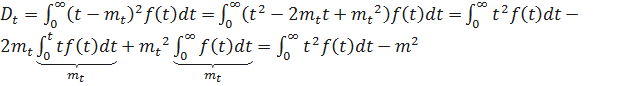 ;
;
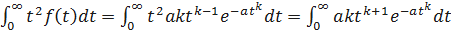 ;
;
Введём новую переменную u вида
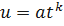 ;
; 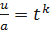 ;
; 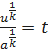 ;
;
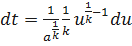 ;
;
если 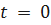 ,то
,то 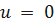 .
.
если 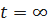 ,то
,то 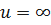 .
.
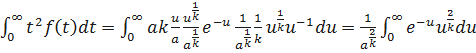 .
.
Известно следующее соотношение для гамма – функции.
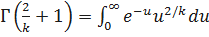 ;
;
Следовательно 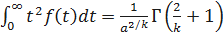 .
.
Тогда
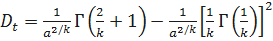 .
.
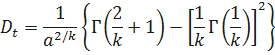
Рассмотрим случай, когда 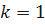 ;
; 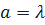 .
.
В этом случае имеем 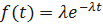 .
.
Т.е. в этом случае имеем экспоненциальный закон надёжности.
Пусть 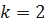 . В этом случае имеем закон Рэлея. Закон Вейбулла лучше описывает время безотказной работы изделия, чем экспоненциальный закон, т.к. в этом случае имеется два параметра: a и k. Пусть
. В этом случае имеем закон Рэлея. Закон Вейбулла лучше описывает время безотказной работы изделия, чем экспоненциальный закон, т.к. в этом случае имеется два параметра: a и k. Пусть 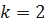 ;
; 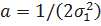 . Тогда имеем
. Тогда имеем 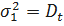 ;
;
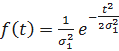 - закон распределения Рэлея.
- закон распределения Рэлея.
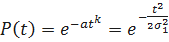 ;
; 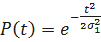 ;
;
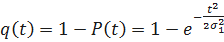 ;
;
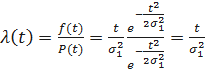 ;
;
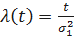 ;
;
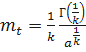 ;
; 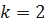 ;
; 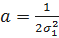 ;
; 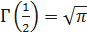 ;
;
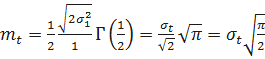 ;
;
Дата добавления: 2015-08-11; просмотров: 1449;
