Критерий Колгомотова

Критерий Павлова можно применять как для непрерывных, так и для дискретных случайных величин. Критерий Колмогорова применяется только для непрерывных случайных величин.

При использовании критерия Колмогорова сравниваются статистическая функция распределения q^*(t) случайной величины Tи выбранная теоретическая функция распределения q(t). Предполагается, что значения параметров функции q(t) известны.

Если параметры теоретической функции распределения q(t) неизвестны, то вместо параметров могут использоваться оценки этих параметров, полученные по результатам опытов, т.е. по статистической выборке. В этом случае принимают .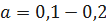

Определяем

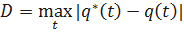
Определяем величину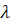

;

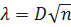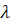- случайная величина.

Выдвигаем гипотезу Hо том, что выбранная нами теоретическая функция распределения q(t) не противоречит статистической функции распределения .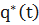

Колмогоров доказал следующую теорему.

Если верна гипотеза H, то при 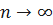независимо от вида функции q(t) случайная величина 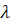имеет функцию распределения вида

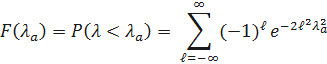
тогда

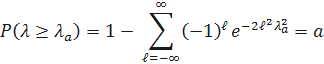
Методика проверки гипотезы Hпо критерию Колмогорова;

1) Определяем статистическую функцию распределения q*(t);

2) определяем ;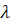

3) Для заданного 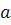определяем 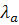по таблице распределения Колмогорова.

Если 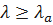, то проверяема гипотеза H отклоняется, т.е. выбранная теоретическая функция распределения q(t) не согласуется (противоречит) статистической функции распределения q*(t).

Если 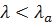, то проверяема гипотеза Hпринимается, т.е. теоретическая функция распределения q(t) не противоречит функции распределения q*(t).

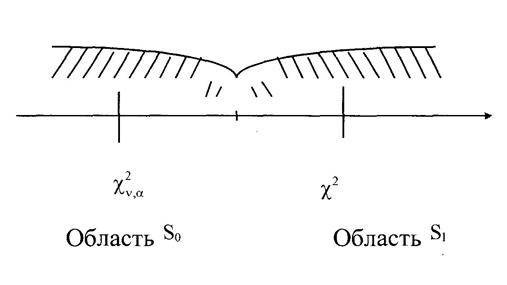
S₀ – область принятия гипотезы H,

S₁ – область отклонения гипотезы H.