Характеристики ремонтопригодности

Рассмотрим систему длительного (многократного) использования. Вэтом случае система после отказа восстанавливается и затем продолжаетфункционировать.

Время восстановления системы T_B- суммарное время обнаружения иустранения отказов.

T_B зависит от многих факторов, имеющих случайный характер (видотказа, тип и число отказавших элементов).

T_B - случайная величина.

Ремонтопригодность системы характеризуется следующимивероятностными характеристиками:

1) вероятность выполнения ремонта в заданное время P_B(t);

2) вероятность невыполнения ремонта в заданное время q_B(t);

3) плотность вероятности времени восстановленияf_B(t);

4) интенсивность восстановления μ(t);

5) среднее время восстановления m_tB;

6) дисперсия времени восстановленияD_tB.

Вероятность выполнения ремой ia в заданное время - это вероятностьтого, что отказ изделия будет устранён в течении заданного t

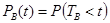
Вероятность невыполнения ремонта в заданное время – этовероятность того, что отказ изделия не будет устранен в течении заданноговремени t

.

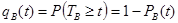Плотность вероятности времени восстановленияf_B(t) равна

.

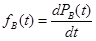Событие A - отказ изделия не устранен на интервале времени от 0 до t.

Событие В - отказ изделия не устранен на интервале времени отtдоt₁.

AВ - произведение событий А и В. Произведением событий А и Вявляется событие, заключающееся в совместном появлении этих событий

Р(АВ) = Р(А) Р(В/А).

Р(В/А) - условная вероятность события В при условии, что событие Апроизошло (имело место).

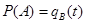- вероятность того, что отказ изделия не устранён наинтервале времени от 0 до t.

Р(В/А) = Р(АВ) / Р(А).

Вероятность Р(АВ) есть вероятность того, что отказ изделия не устранен на интервале

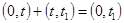
т.е.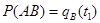

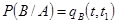- вероятность того, что отказ изделия не устранён наинтервале времени 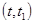при условии, что отказ изделия не был устранён на интервале времени от 0 до t.

Таким образом

;

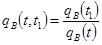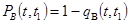- вероятность того, что отказ изделия будет устранённа интервале времени 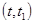при условии, что отказ изделия не был устранён на интервале времени от 0 до t.

.

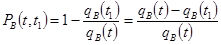Пусть 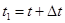; тогда

;

;

;

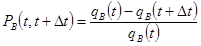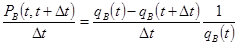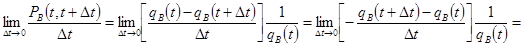
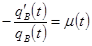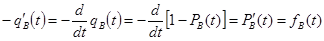
Таким образом: ;(*)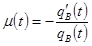

или: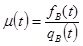

Из(*) имеем ;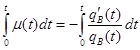

или ;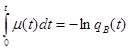

или ;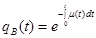

;

;

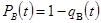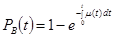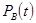- вероятность выполнения ремонта в заданное время.

При 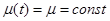получаем экспоненциальный закон ремонтопригодности

Определим среднее время восстановления :

;

;

;

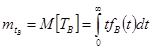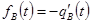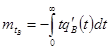Этот интеграл можно вычислить по частям

u = t; ;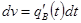

du = dt; ;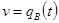

;

;

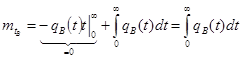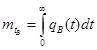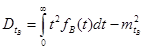-дисперсиявремени восстановления

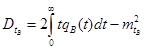
В случае экспоненциального закона ремонтопригодности имеем:

; .

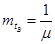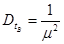1.12 Экспериментальная оценка надёжности изделий

Для решения теоретических и практических задач надёжности необходимо знать законы распределения исходных случайных величин. При оценке надёжности изделий может решаться задача определения по данным эксплуатации или специальных испытаний среднего времени безотказной работы 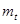, среднего времени восстановления .

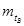Рассмотрим случайную величину Т - время безотказной работы. Приэксплуатации или испытаниях изделий в течении определённого временислучайная величина Т может принять п различных значений. Совокупностьэтих значений случайной величины Т называется статистической выборкойобъёма n. Эта выборка может использоваться для статистической оценкизакона распределения случайной величины Т.

Приведём пример статистической выборки для 10 однотипныхизделий.

При большом числе n удобнее перейти от статистической выборки кстатистическому ряду. Определяем диапазон значений случайной величиныТ.

,

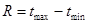где , 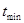- максимальное и минимальное значение случайной величины Т.

Этот диапазон R разбивается на интервалы длины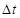

;

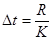где К- количество интервалов. Целесообразно выбирать число интервалов порядка 10 - 20. Обозначим через 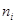количество значений случайной величины Т, попавших в интервал i - й длины 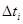. Полагаем 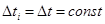; i=1,2,…,K.

Определим частоту попадания в i - й интервал

.

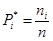Определяем статистическую плотность вероятности времени безотказной работы Т

.

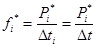Результаты сведём в таблицу:

Наглядное представление о законе распределения случайной величины Т дают статистические графики. Из них самые распространённые: полигон, гистограмма, статистическая функция распределения.

Полигон строится следующим образом: на оси абцисс откладываютсяинтервалы 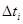, i= 1, 2,…,k , в серединах интервалов строятся ординаты,равные частотам 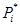и концы ординат соединяются.

Построение гистограммы: над каждым интервалом 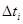, i= 1, 2,…,kстроится прямоугольник, площадь которого равна частоте 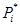в этом интервале.

Построение статистической функции распределения случайной величины Т. Над каждым интервалом проводится горизонтальная линия на уровне ординаты, равной величине накопленной частоты.

Второй способ построения статистической функции распределения случайной величины Т:

,

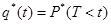где 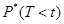- частота выполнения события Т<t.

,

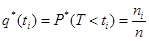где 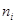- число опытов, при которых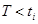

Статистическая плотность вероятности ^ и статистическая функцияраспределения 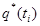случайной величины Т представляют статистический закон распределения случайной величины Т.