Определение интенсивности отказов A.(t) по результатам испытаний
Интенсивность отказов λ(t) может быть определена по результатам испытаний. Пусть на испытания поставлено N изделий. Пусть n(t) – число изделий, не отказавших к моменту времени t. Тогда:
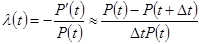 ;
;
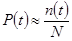 ;
; 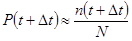 ;
;
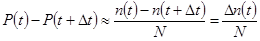 ;
;
где ∆n(t) - число отказавших изделий на интервале времени (t, t + ∆t). Тогда:
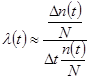 или
или 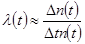
1.10 Числовые характеристики надёжности
Рассмотренные количественные характеристики надёжности являются функциями времени. Для определения этих характеристик на основе опытных данных с достаточной точностью требуется большой объём испытаний. Более просто найти числовые характеристики надёжности. К ним относятся:
1) среднее время безотказной работы;
2) дисперсия времени безотказной работы;
Определим среднее время безотказной работы или математическое ожидание случайной величины Т. Имеем
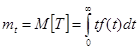
Величина 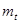 также называется средняя наработка на отказ.
также называется средняя наработка на отказ.
Известно, что 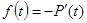 . Тогда:
. Тогда:
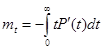 .
.
Этот интеграл можно вычислить по частям
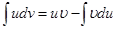 ;
;
u=t; 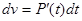 ;
;
du=dt; v = P(t);
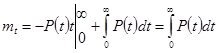 ;
;
т.к. P(t) при 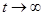 убывает быстрее, чем растёт t.
убывает быстрее, чем растёт t.
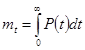
Для экспоненциального закона надёжности имеем:
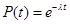 ;
;
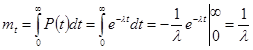 .
.
Итак, для экспоненциального закона надёжности среднее время безотказной работы есть величина, обратная интенсивности отказов.
Приближённое значение 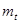 можно определить по формуле
можно определить по формуле 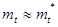 , где
, где
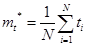
Здесь ti- время безотказной работы i - го изделия; N- общее число изделий, поставленных на испытания.
Определим дисперсию времени безотказной работы. Имеем
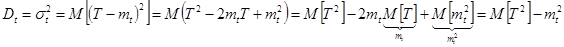 ;
;
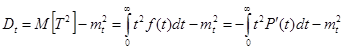 .
.
Интеграл берём по частям
u = t2; dv = P'(t)dt;
du = 2tdt; v = P(t);
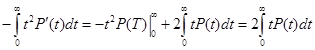 ;
;
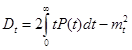
Для экспоненциального закона надёжности имеем:
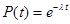 ;
; 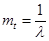 ;
;
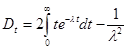 .
.
Интеграл берём по частям:
u = t; dv = 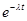 dt;
dt;
du = dt; 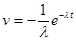 ;
;
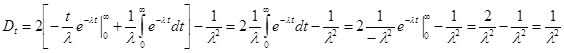 ;
;
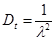 ;
; 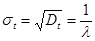 ;
;
Дисперсия Dtхарактеризует степень разброса значений относительно 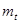 .
.
На основании результатов испытаний можно определить приближённое значение дисперсии
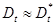 ;
;
где 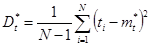 .
.
Дата добавления: 2015-08-11; просмотров: 1146;
