Плотность вероятности f(t) времени безотказной работы Т

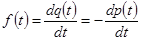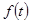; - частота отказов.

Здесь 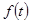- плотность вероятности случайной величины Т или частота отказов.

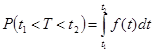→ вероятность того, что отказ изделия произойдёт

на интервале времени .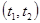

Для плотности вероятности времени безотказной работы Тсправедливо приближённое равенство:

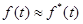, где - оценкачастотыотказов.

Здесь N - число изделий, поставленных на испытания, 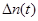- числоотказавших изделий на участке времени (t, t + ∆t).

1.9 Интенсивность отказов λ(t)

Рассмотрим вероятность безотказной работы изделия на промежуткевремени от t до t₁ при условии, что изделие до момента времени t неотказывало.

Обозначим эту вероятность через .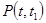

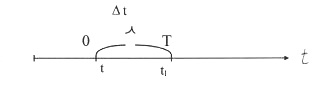
Событие А - изделие работало безотказно на интервале, времени от 0 до t.

Событие В - изделие работало безотказно на интервале времени от tдо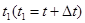

АВ - произведение событий А и В. Произведением событий А и Вявляется событие, заключающееся в совместном появлении этих событий.

Р(АВ) = Р(А) Р(В/А).

Р(В/А) - условная вероятность события В при условии, что событие Апроизошло (имело место).

Р(А) = P(t) - вероятность безотказной работы изделия на интервалевремени от 0 до t

Р(В/А) = Р(АВ) / Р(А); Р(В/А) =P .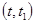

Но вероятность Р(АВ) есть вероятность безотказной работы изделия наинтервале

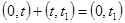; т.е. .

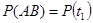Поэтому

.

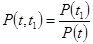Вероятность отката изделия на интервале 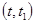равна

;

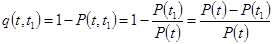Так как 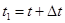, то

;

;

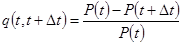
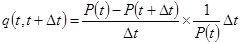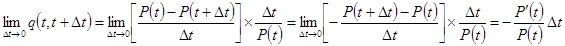Введём обозначение

;

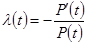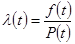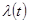; - интенсивность отказов.

Прималом ∆tимеем

.

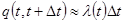Отсюда .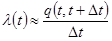

Из (1.3) видно, что интенсивность отказов представляет собойотношение вероятности отказа на интервале (t, t + At) к длине этогоинтервала (при малом ∆t).

Из (1.1) имеем

.

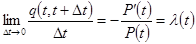Из (1.2) имеем

.

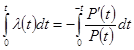Отсюда ;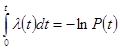

или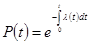

; ;

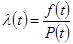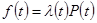или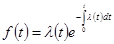

Для практически важного частного случая 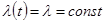; формула принимает вид

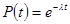
Формула называется экспоненциальным законом надёжности. На практике этот закон ввиду его простоты нашёл широкое применение при расчёте надёжности изделий.

График функции λ(t):

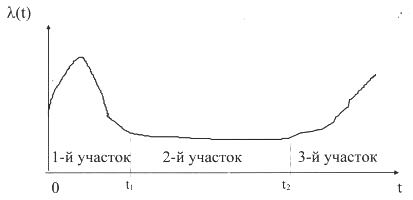
1 - й участок - период приработки изделия.

2-й участок - период нормальной работы.

3-й участок - период старения или износа изделия.