Уравнения Эйлера и уравнение Бернулли для сжимаемой жидкости.

Динамика сжимаемой жидкости базируется также на 2-м законе Ньютона, записанном для единицы массы жидкости. Равнодействующая сил давления и внешних сил создает ускорение единицы массы, поэтому

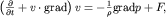
(3.35)

где F - внешняя сила, действующая на единицу массы. Для определения 5-ти неизвестных величин (v_x, v_y, v_z, p и ) необходимо дополнить (3.35) материальным уравнением, связывающим плотность и давление:

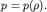
(3.36)

Система (3.34) - (3.36) носит название уравнений Эйлера для сжимаемой жидкости. Огромное количество задач газодинамики решается на основе анализа этих уравнений.
Воспользуемся уравнением (3.35) и получим уравнение Бернулли. Для этого видоизменим правую часть (3.35), введя вспомогательную функцию 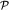(2.27), и учтем (2.29). Тогда (3.35) примет вид

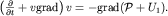
(3.37)

При стационарном течении 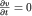. В направлении оси трубки тока (вдоль криволинейной координаты ) можно записать

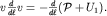
(3.38)

Поскольку потенциальная энергия единицы массы 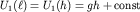, а 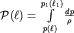, то, по аналогии с (3.13), перепишем (3.38) в виде:

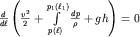
(3.39)

Интегрируя (3.39) вдоль трубки тока, получаем уравнение Бернулли для сжимаемой жидкости

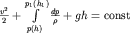
(3.40)

Здесь h - положение по вертикали сечения трубки тока с координатой . Очевидно, что 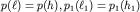. Постоянная в (3.40) определяется заданием скорости v₁ и высоты h₁ в фиксированном сечении с координатой 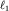. С учетом этого, уравнение (3.40) обретает вид

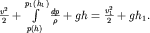
(3.41)

Для практического использования уравнения Бернулли необходимо знание материальной связи между p и . Для случая несжимаемой жидкости ( = const) уравнение (3.41) переходит в (3.15).
Если речь идет о потоке газа, то при его быстром сжатии (увеличение плотности) газ будет нагреваться. Из-за плохой теплопроводности газа тепло не будет успевать уходить из нагретых областей. Поэтому для установления материальной связи 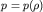воспользуемся адиабатическим приближением:

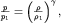
(3.42)

где показатель адиабаты 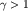. Такая связь получается из первого начала термодинамики и уравнения состояния идеального газа (2.32) при условии отсутствия теплообмена между нагретой областью и окружающей средой. Давление в (3.42) возрастает с плотностью быстрее, чем при изотермическом процессе, так как 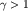. В курсе молекулярной физики будет показано. что 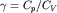(C_p и C_V - теплоемкости при постоянных давлении и объеме соответственно). Для воздуха, состоящего главным образом из двухатомных газов, = 1,4.
Если подставить (3.42) в (3.41) и выполнить простейшее интегрирование, то можно записать выражение для распределения давления вдоль трубки тока:

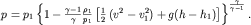
(3.43)

Не умаляя общности, будем считать трубку тока горизонтальной (h=h₁). Положим далее скорости течения такими, что

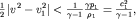
(3.44)

где 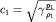- параметр, имеющий размерность скорости. Как мы увидим несколько позднее, скорость звука в газе

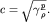
(3.45)

При нормальных условиях для атмосферы с=336 м/с. В этом случае (3.43) можно разложить в ряд:

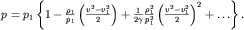
(3.46)

Если пренебречь квадратичным членом в (3.46), то распределение давлений соответствует течению несжимаемой жидкости с плотностью 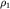=const. Квадратичный член начинает давать вклад в распределение давлений при скоростях потока, соизмеримых со скоростью звука с₁.
Подставив (3.42) в (3.43), получаем распределение плотности вдоль трубки тока:

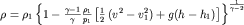
(3.47)

Для горизонтальной трубки тока и при условии (3.44) распределение плотности (3.47) имеет вид:

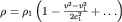
(3.48)

Таким образом, изменение плотности газа необходимо принимать в учет только при скоростях течения, сопоставимых по порядку величины со скоростью звука, определяемой, как следует из (3.45), давлением и плотностью в этом потоке.
Если же скорость течения 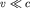, то сжимаемостью газа можно пренебречь и оперировать с ним, как и с жидкостью.