Уравнение неразрывности для сжимаемой жидкости

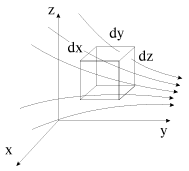
При течении газов, особенно при больших скоростях, их плотность может заметно, а то и значительно, меняться во времени и в пространстве. Ясно, что объем втекающей жидкости может не быть равным объему вытекающей жидкости через поверхность кубика, изображенного на рис. 3.11. Если такого равенства нет, то масса газа внутри кубика (а с ней и плотность) будут со временем меняться. Уравнение (3.24) в этом случае становится несправедливым. Однако и здесь можно записать уравнение неразрывности, основная идея вывода которого базируется на балансе массы газа, составляющего физическую суть равенства (3.1). Поток массы газа через площадку dSбудет равен 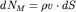. Тогда полный поток массы газа через боковую поверхность элемента объема dxdydz, аналогично (3.27), равен

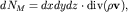
(3.32)

где - 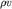новое векторное поле. Если этот поток положительный, то масса внутри элемента 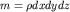будет убывать за счет уменьшения во времени плотности . Поэтому, записывая условие баланса массы в виде

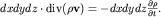
(3.33)

мы получаем (после сокращения на dxdydz) одно из фундаментальных уравнений гидродинамики - уравнение неразрывности сжимаемой жидкости:

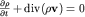
(3.34)

Следует отметить, что при =const это уравнение переходит в (3.24).

Рис. 3.11.

В электродинамике это уравнение является также фундаментальным. В самом деле, если речь идет о движущихся зарядах, объемная плотность которых равна , то уравнение (3.34) является математическим выражением универсального закона сохранения заряда.