Закон Паскаля.

Если пренебречь вначале силами тяготения, действующими на каждую частицу жидкости (или силами инерции, если таковые существуют), то из простейших соображений относительно условий равновесия элемента жидкости следует, что

при этом давление p, являющееся скалярной величиной, одинаково во всех точках объема, занятого покоящейся жидкостью. Условие (2.1) автоматически обеспечивает не только равенство нулю суммы сил давления, приложенных к данному элементу, но равенство нулю суммарного момента этих сил.
Для его доказательства рассмотрим неподвижную жидкость, помещенную в цилиндрический сосуд сечением S₁, закрытый сверху поршнем (рис. 2.1, левый сосуд). Если надавить на поршень с силой F₁, то в жидкости будут созданы внутренние напряжения (давления). На единицу поверхности элемента жидкости будет действовать сжимающая сила f_ii = - p_iin_i, направленное противоположно внешней нормали n_i к i-ой поверхности (на рис. 2.1 изображены только две силы).

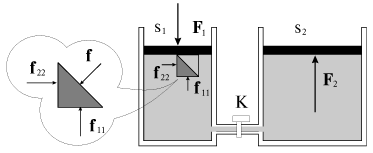
Рис. 2.1.

Поскольку силы, действующие на противоположные грани кубика, равны по величине, то p₁₁=F₁/S₁. Равенство давлений p₁₁ и р₂₂ следует из условия равновесия половины кубика, выделенного более темным цветом и изображенного на фрагменте. Действительно, f₁₁=f₂₂=f/ 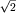, поэтому р₂₂=р₁₁. Рассматривая равновесие элементарных объемов в различных точках жидкости, получим условие:

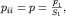
(2.2)

которое и является математическим выражением закона Паскаля.
Если этот сосуд соединить при помощи трубки с другим цилиндрическим сосудом сечением S₂, то при открывании крана K внутренние напряжения по жидкости, находящейся в соединительной трубке, в соответствии с законом Паскаля передадутся во второй сосуд (рис. 2.1). На поршень, его закрывающий, жидкость будет давить вверх с силой

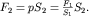
(2.3)

Если S₂>S₁, то развиваемое усилие F₂>F₁. Этот выигрыш в силе используется во многих гидроприводящих устройствах (гидроприводах): в приводе ковша экскаватора, рулей ракет и самолетов. На этом же принципе работает гидравлический пресс, гидравлический домкрат и т.д.
В системе СИ за единицу давления принимается Паскаль (Па), при этом 1Па=1Н/1м². В технике в качестве единицы давления используется техническая атмосфера: 1ат=1кГс/1см²=9,8*10⁴ Па.

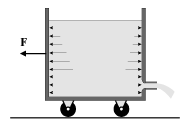
Интересно отметить, что трубки тока жидкости расположены преимущественно ближе к стенке сосуда с отверстием, в то время как у противоположной (левой на рис. 3.8) стенки жидкость практически малоподвижна. Это означает, что на левую стенку действуют силы давления, которое легко посчитать, используя линейный закон нарастания гидростатического давления с глубиной, даваемой формулой (2.11). Расчет сил давления, действующих на правую стенку, требует гидродинамического решения задачи. Однако и без такого расчета ясно, что в трубке тока, примыкающей к правой стенке, давление на каждой глубине будет меньше соответствующего этой глубине гидростатического давления. Это означает, что равнодействующая сил давления, действующих на обе стенки, направлена в сторону, противоположную направлению истечения жидкости. Под действием этой силы, называемой также реактивной, сосуд, поставленный на колеса, может придти в движение. Величину этой силы легко посчитать с использованием формулы Торичелли. По 3-му закону Ньютона искомая реактивная сила равна по величине силе, с которой стенки сосуда действуют на воду, сообщая ее (по 2-му закону Ньютона) приращение импульса в направлении истечения. Поскольку масса, вытекающая через отверстие с сечением S равна 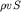, то изменение импульса в единицу времени составит величину 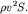Поэтому реактивная сила

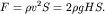
(3.19)

Рис. 3.8.

Отметим, что если бы мы ошибочно приняли, что распределение давлений с глубиной у правой стенки было такое же, как у левой, то реактивная сила получилась бы вдвое меньшей:

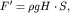
(3.20)

где 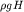- величина гидростатического давления на глубине H, S - площадь отверстия в правой стенке.
Однако можно добиться одинакового (гидростатического) распределения давлений у обеих стенок, если конец трубки с острой кромкой будет отстоять от правой стенки, как показано на рис. 3.9. В этом случае реактивная сила может определяться с помощью формулы (3.20). Если же ее вычислять при помощи (3.19), то в этой формуле надо вместо сечения трубки S подставить сечение струи воды в трубке S_B=kS, где коэффициент истечения k 1/2. При таком истечении трубка будет заполнена жидкостью приблизительно наполовину.

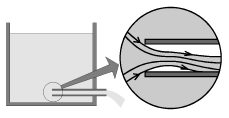
Рис. 3.9.

Реактивную силу можно увеличить, если прежде всего повысить скорость истечения жидкости. Для этого следует использовать замкнутый сосуд с отверстием, при этом над свободной поверхностью жидкости создается давление p₁>p₀. Тогда скорость истечения жидкости из уравнения Бернулли получается равной:

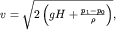
(3.21)

а реактивная сила возрастает линейно с повышением избыточного давления 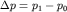над свободной поверхностью жидкости

.