Теорема Штейнера. Для установления связи между моментом инерции тел относительно двух параллельных осей применяется теорема Штейнера:

Для установления связи между моментом инерции тел относительно двух параллельных осей применяется теорема Штейнера:

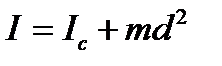(4)

где 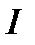- момент инерции относительно новой оси

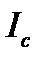- момент инерции относительно центра масс

d – расстояние между осями

1. Момент силы,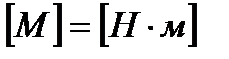

Вектором момента силы относительно полюса называют векторное произведение радиус-вектора и вектора силы:

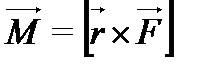(5)

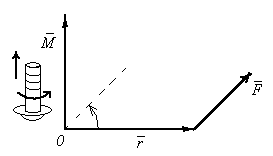Направление вектора момента силы находится по правилу правого винта (см. рис): перенесем вектор 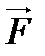параллельно самому себе так, чтобы совпадали начала векторов 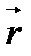и 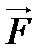. Если вращать головку винта в направлении от вектора 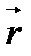к вектору 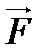, то поступательное движение винта укажет направление вектора момента силы .

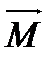Модуль вектора момента силы равен:

, (6)

где - угол между радиус-вектором и линией действия силы.

Момент равнодействующей силы относительно полюса О равен геометрической сумме векторов моментов составляющих сил относительно того же полюса:

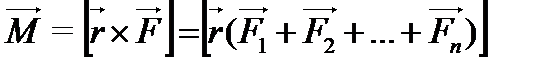(7)

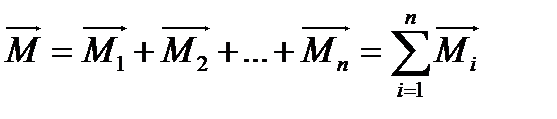или (8)

1. Момент импульса материальной точки,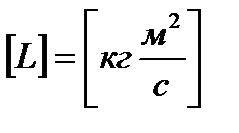

Вектором момента импульса м.т. относительно полюса О называют векторное произведение радиус – вектора 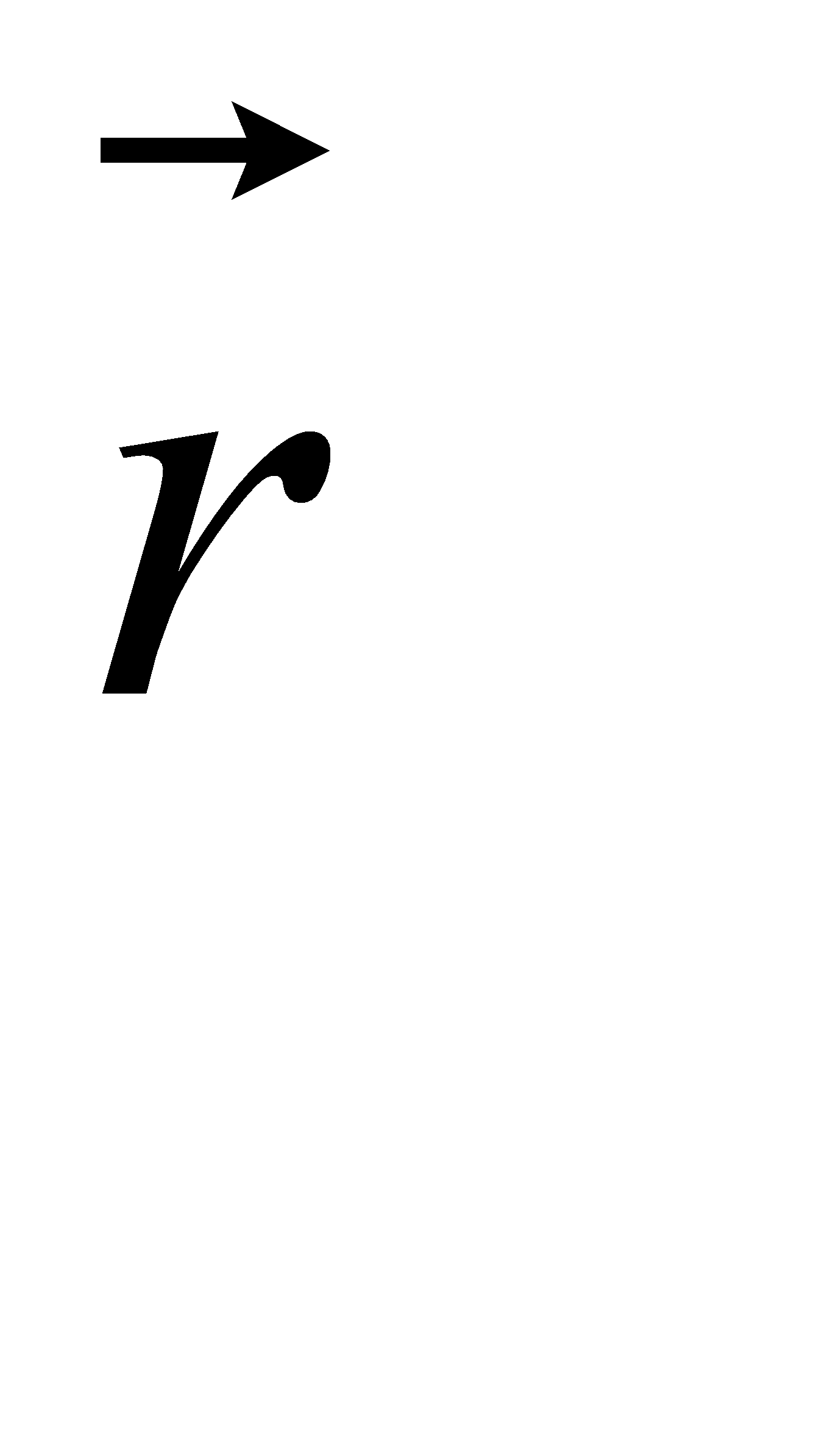и вектора импульса 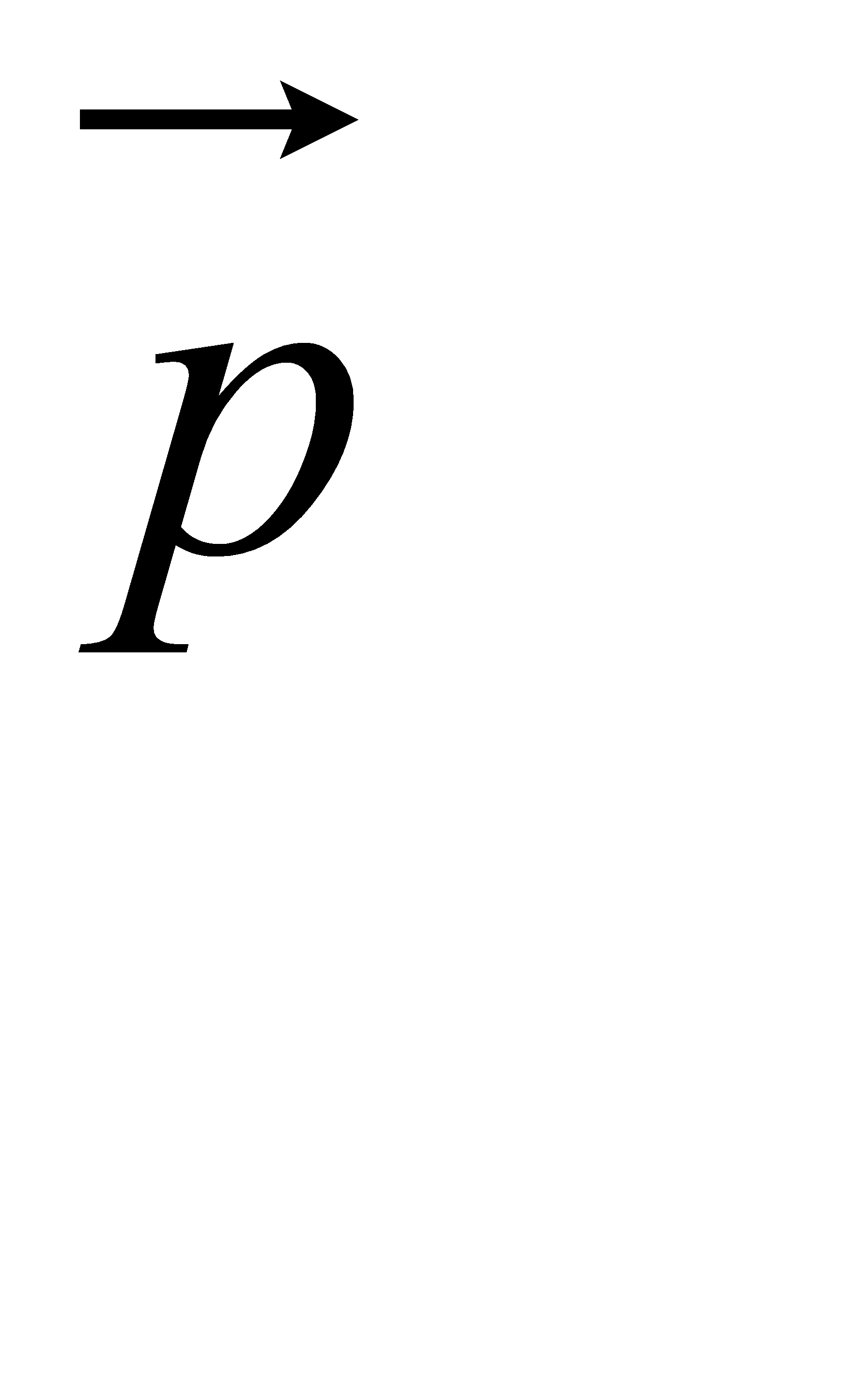относительно этого же полюса.

Радиус-вектор 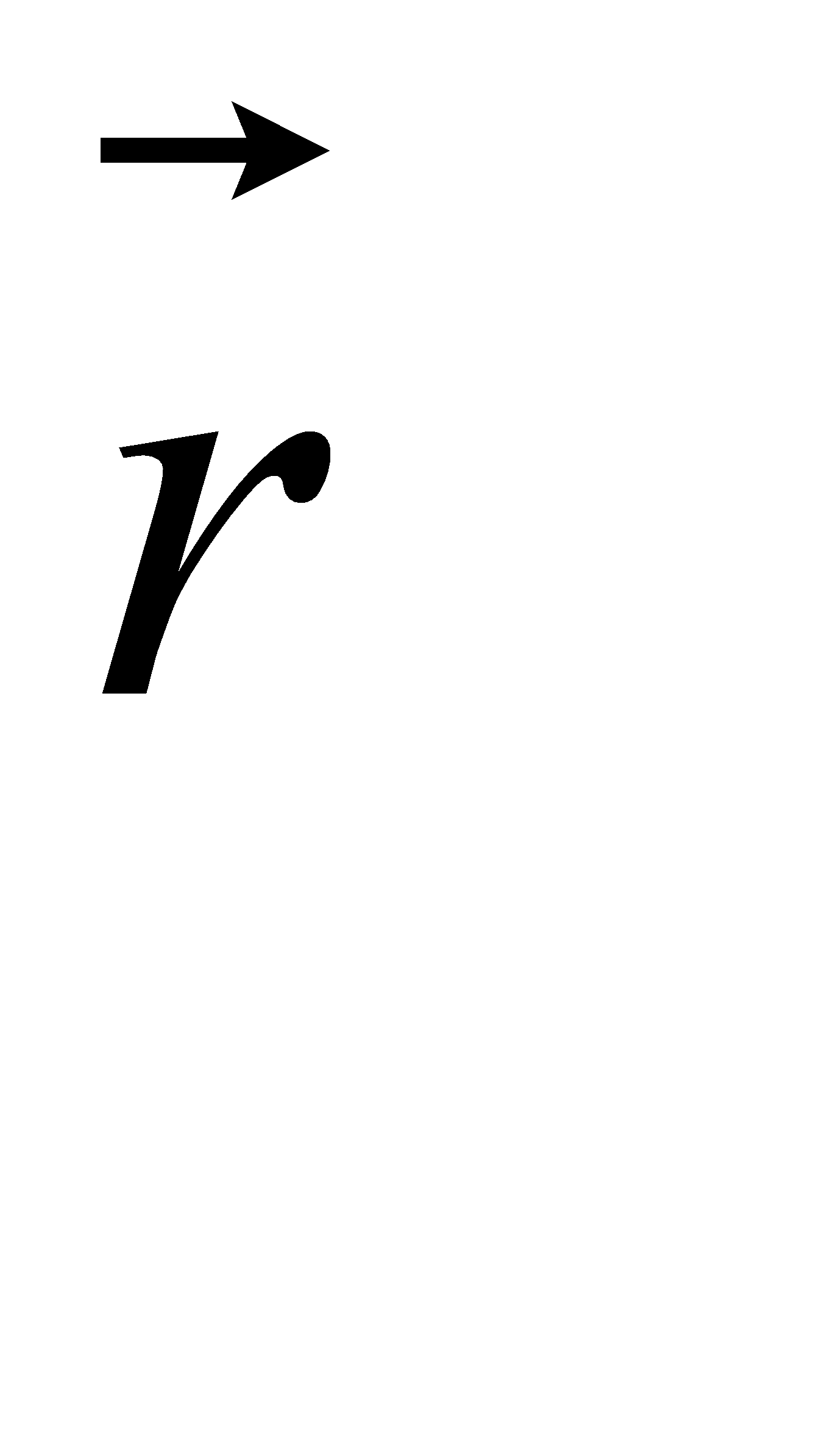проводится от полюса О до м. т.

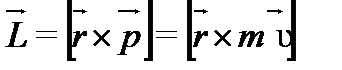(9)

Направление вектора момента импульса находится по правилу правого винта и совпадает с вектором угловой скорости.

Если учесть, что 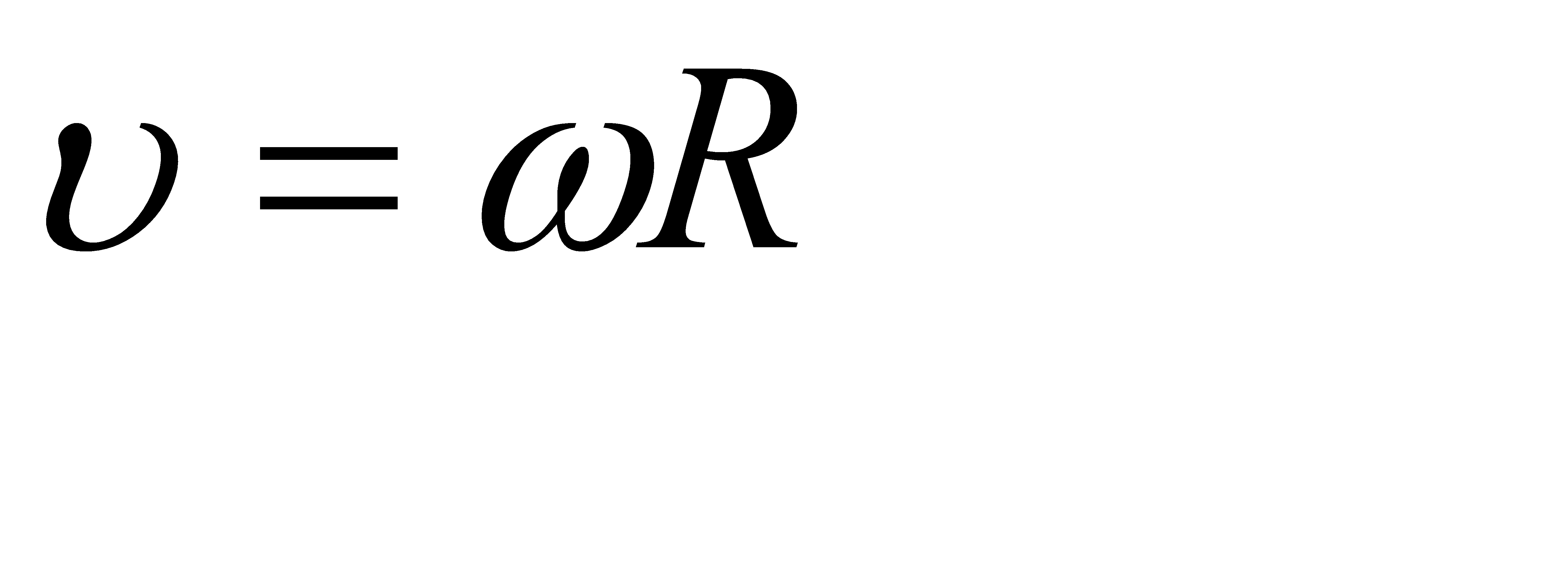, тогда момент импульса равен: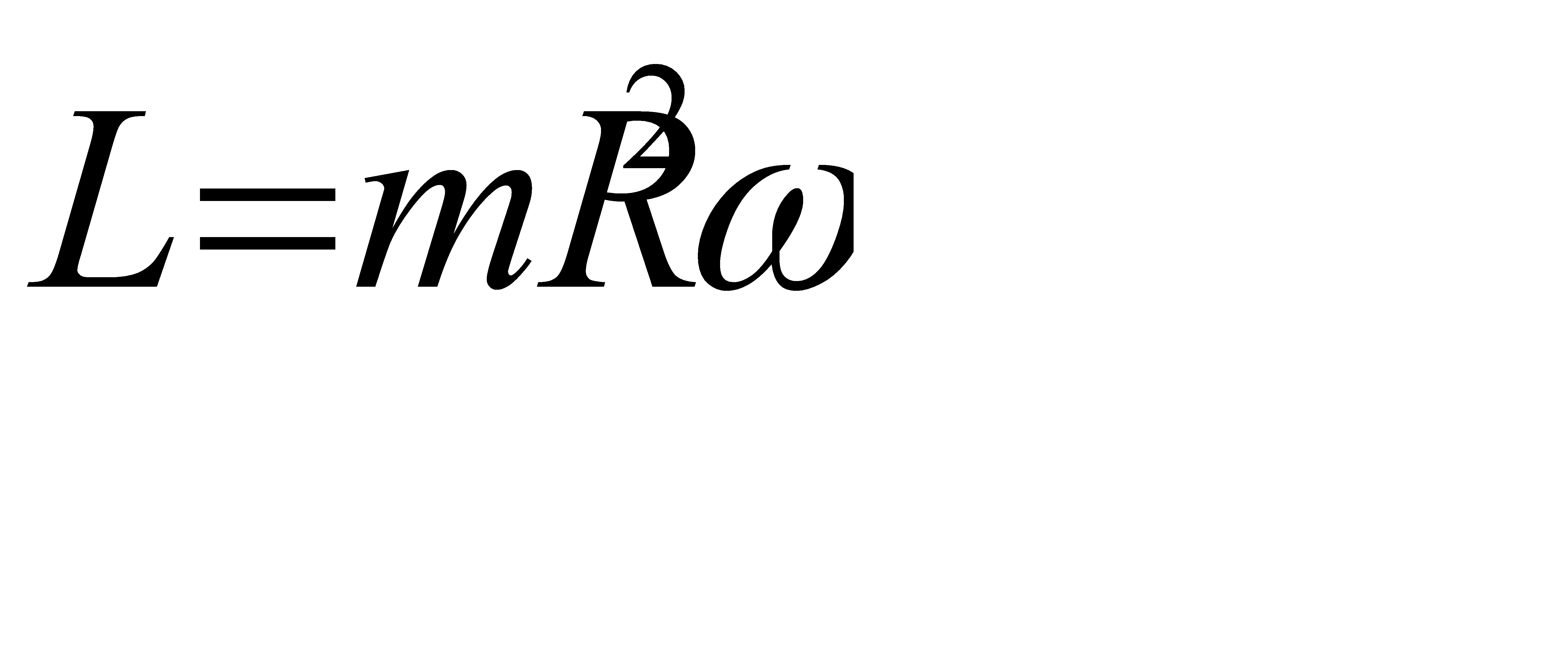

или 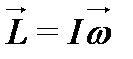(10)

Момент количества движения твердого тела относительно оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость.

Модуль вектора момента импульса равен:

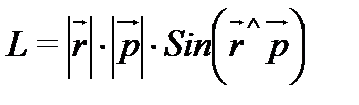, (11)

Вектор момента импульса системы м.т. от-но полюса О равен геометрической сумме векторов моментов импульса, действующих на каждую точку в отдельности от-но того же полюса О:

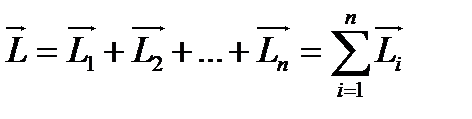(12)

или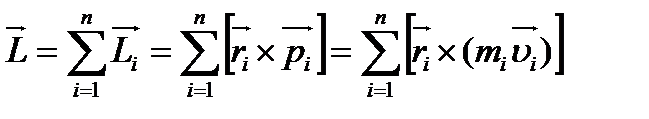

Согласно уравнению (5.8) второй закон Ньютона для вращательного движения

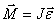
По определению угловое ускорение и тогда это уравнение можно

переписать следующим образом

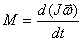
с учетом (5.9)

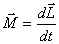
или

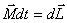
(5.10)

Это выражение носит название основного уравнения динамики вращательного движения и формулируется следующим образом: изменение момента количества движения твердого тела 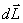, равно импульсу момента 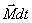всех внешних сил, действующих на это тело.