Лекция 5. Закон сохранения момента импульса.

Момент импульса вращающегося тела

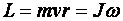, (1.47)

где 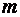– масса тела; 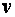– скорость; 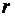– радиус орбиты, по которой перемещается тело; 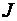– момент инерции; 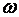– угловая скорость вращающегося тела.

Закон сохранения момента импульса:

– для вращательного движения

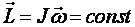при ;

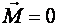закон сохранения импульса:

– для поступательного движения

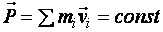при .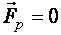

Для того чтобы изменить скорость при поступательном движении, необходимо обязательно приложить силу.

Угловую скорость можно изменить, не прикладывая силы или момент силы, достаточно изменить момент инерции. Так, фигурист, прижимая руки к телу, уменьшает момент инерции и его угловая скорость увеличивается.

Если, например, в замкнутой системе у вращающегося тела момент инерции уменьшится до величины 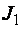, то скорость вращения этого тела возрастет (станет 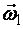₁,), т. е.

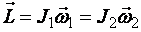. (1.48)

Выражение (1.48) является законом сохранения момента импульса.

При вращательном движении скорость изменения момента импульса материальной точки равна моменту силы (при неизменном моменте инерции)

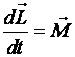. (1.49)

Наряду с законами сохранения импульса и энергии, закон сохранения момента импульса является одним из важнейших фундаментальных законов физики.

Важным случаем является вращение твердого тела вокруг неподвижной оси. В этом случае момент инерции 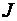при вращении остается постоянным и уравнение (1.49) переходит в

.

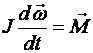При уменьшении момента инерции вращающегося тела его угловая скорость увеличивается (при условии, что момент внешних сил равен нулю). Изменение угловой скорости системы может происходить только за счет работы каких-то сил. Такими силами в нашем примере являются внутренние силы, действующие в системе.

Отметим свойства замкнутой системы, на которую не действуют внешние силы. Если такая система покоится, то за счет внутренних движений (внутренних сил) эту систему невозможно сместить в пространстве (поступательное перемещение).

С помощью одних только внутренних движений можно повернуть систему в пространстве на любой угол [1].

Полагаем, что под действием момента силы 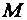тело с моментом инерции 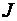вращается с угловым ускорением 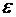( 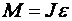). За время 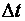угловая скорость изменилась на величину 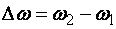– тогда из основного закона динамики вращательного движения следует

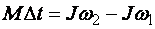. (1.50)

Импульс момента внешних сил, действующих на вращающееся тело, равен изменению его момента импульса.

Величина 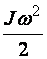для вращательного движения является кинетической энергией. Выражение, аналогичное для поступательного движения записывается следующим образом:

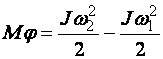, (1.51)

где 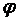– угловой путь, пройденный при воздействии на тело момента сил 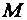; 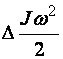– изменение кинетической энергии.