Исследование кривых второго порядка

Исследование кривых второго порядка.

Общее уравнение кривой второго порядка можно представить уравнением

Чтобы определить тип кривой, нужно вычислить дискриминант старших членов

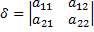
и дискриминант уравнения

Если 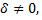то кривая центральная, если 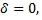то кривая нецентральная.

В зависимости от значений 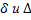общее уравнение кривой определяет следующий геометрический образ,

Таблица 1

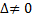
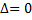
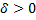
	эллипс	точка
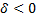
	гипербола	пара пересекающихся прямых
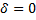
	парабола	пара параллельных прямых

Преобразование центральной кривой.

1) Найдем координаты центра кривой, для чего составим и решим систему

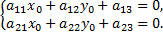
Решение системы будет точка 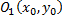– центр кривой.

Необходимо выполнить параллельный перенос начала координат системы в центр кривой – точку После преобразования параллельного переноса общее уравнение кривой второго порядка не будет содержать членов с первыми степенями переменных и 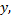а группа старших членов останется неизменной.

Уравнение примет вид

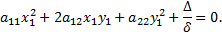
2) Найдем угол поворота системы по формуле

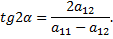
Вычислим

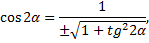
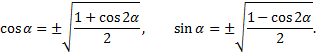
Знак выбирается в соответствии с тем, в какой четверти выбран угол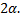

Если при этом вычисление 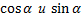окажется затруднительным, то следует, зная найти из таблиц.

Подставить значение 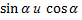в формулы поворота осей координат

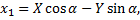
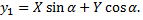
Формулы поворота подставим в уравнение

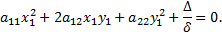
При этом преобразовании в уравнении кривой коэффициент при произведении 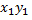обратится в нуль, свободный член останется неизменным.

Уравнение примет вид

Это уравнение, которое приводится к каноническому.

Преобразование нецентральной кривой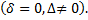

Преобразование кривой параболического типа следует начать с поворота системы координат на угол который находится по формуле

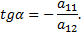
Вычислим 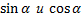по формулам

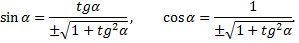
Подставим значения 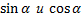в формулы поворота осей координат

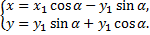
Формулы поворота подставим в заданное уравнение. При этом преобразовании в уравнении кривой коэффициенты пр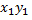и и или при 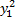обратятся в нуль, а свободный член остается неизменным.

Уравнение кривой примет вид

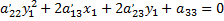
или

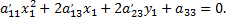
В полученном уравнении выделим квадрат двучлена, т.е. приведем к виду

или

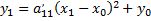
т.е.

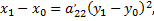
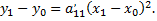
Выполнить преобразование параллельного переноса начала координат в вершину параболы, обозначив

где точка 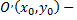вершина параболы, начало координат системы

Уравнение кривой при этом примет вид

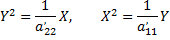
- это каноническое уравнение параболы.

Преобразование нецентральной кривой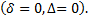

Если 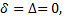то уравнение кривой можно представить в виде

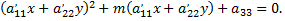
Решив это квадратное уравнение относительно двучлена 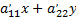получим пару параллельных прямых

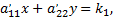
где 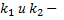корни квадратного уравнения относительно двучлена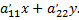

Рассмотрим пример. Преобразовать к каноническому виду и построить кривую

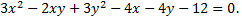
Вычислим дискриминант старших членов

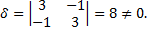
Вычислим дискриминант уравнения

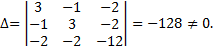
Вывод: 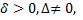следовательно, кривая центральная-эллипс.

Выполним преобразование параллельного переноса начала координат в центр кривой, координаты которого найдем из системы

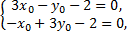
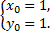
Центр кривой – точка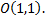

Уравнение примет вид

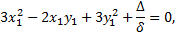
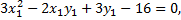
данное уравнение не содержит членов с первыми степенями 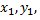группа старших членов остается неизменной.

Выполним преобразование поворота осей координат, на угол которой найдем по формуле

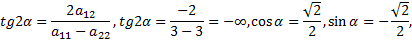
Формулы поворота осей координат примут вид

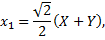
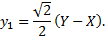
Подставим их в уравнение кривой, получим

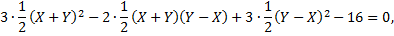
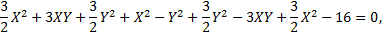
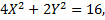
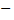каноническое уравнение эллипса, где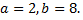

Найдем точки пересечения кривой с осью 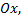для чего решим систему

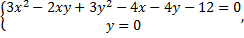
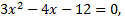
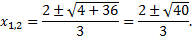
Точки пересечения

Выполним построение

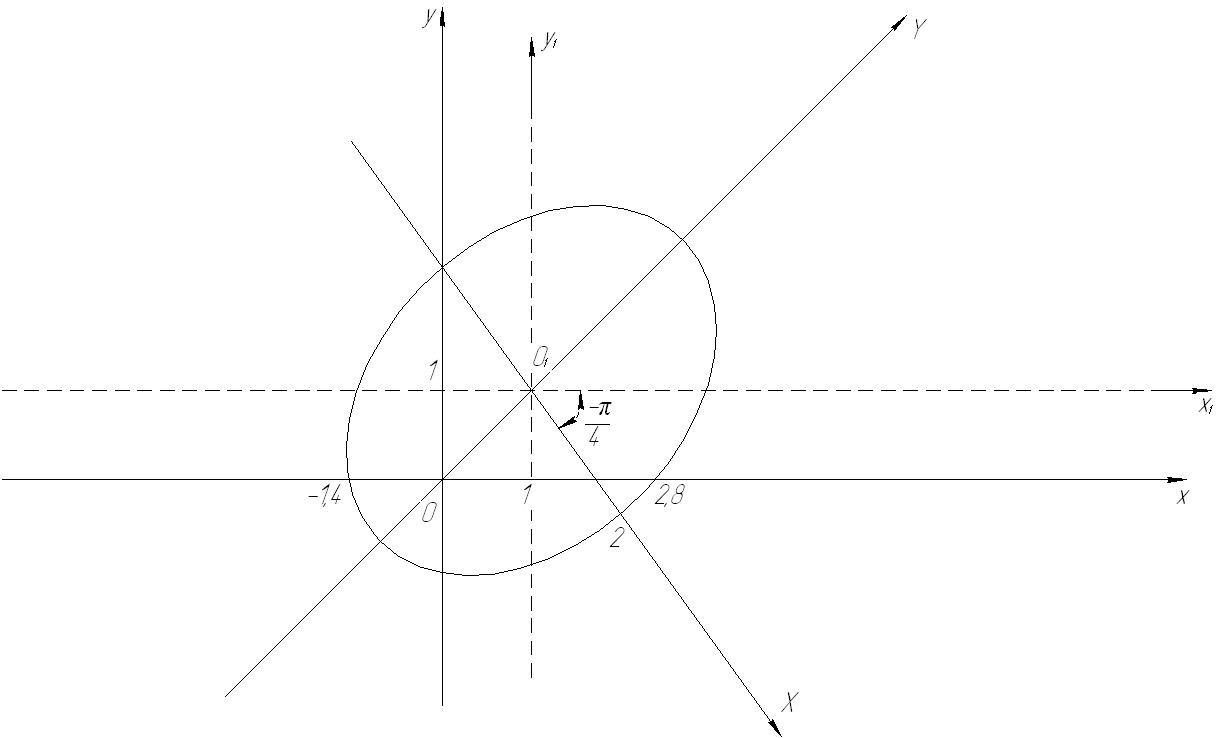
Рис. 20

Контрольные вопросы

1. Записать каноническое уравнение окружности и ее основные характеристики.

2. Записать каноническое уравнение эллипса и перечислить его характеристики.

3. Записать каноническое уравнение гиперболы и назвать ее характеристики.

4. Записать каноническое уравнение параболы.

5. Знать схему исследования кривых второго порядка.