Прямая в пространстве.
Определение: Любой ненулевой вектор, параллельный прямой, называется направляющим вектором этой прямой.
l= (m; n; p) ║прямой.
Пусть т. М0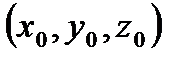 
- произвольная фиксированная точка прямой,
т. М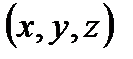 
- текущая фиксированная точка прямой.
Вектор М0М=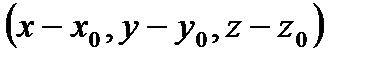 
║ l= (m; n; p).
Координаты векторов М0М и l пропорциональны.
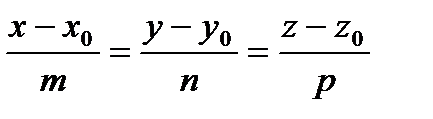- каноническое уравнение прямой в пространстве.
Положим в канонических уравнениях все равно параметру t и выразим x, y, z:
.
; 
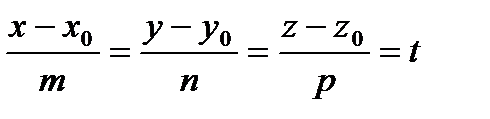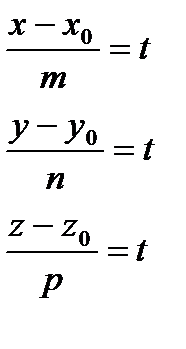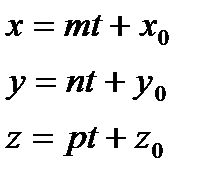- параметрические уравнения прямой в пространстве.
Задавая различные значения параметра t из параметрических уравнений можно получать точки, принадлежащие прямой.
Аксиома: Через две различные точки проходит одна прямая.
| a |
| M(x, y, z) |
| M2(x2, y2, z2) |
| M1(x1, y1,z1) |
| l |
Прямая а проходит через М1, М2. М1М и М1М2 – направляющие векторы.
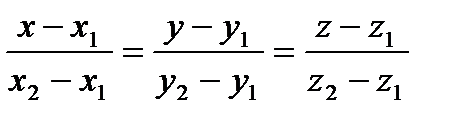- уравнение прямой, проходящей через две точки.
Дата добавления: 2015-08-11; просмотров: 668;