Задание вектора в пространстве.
Любой вектор в пространстве имеет длину и направление.
Длина вектора │а│= 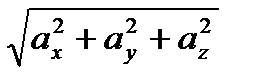 .
.
Направление вектора задают три направляющих косинуса: cos α, cos β, cos γ, где Ðα- угол между 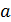 и ОХ, Ðβ- угол между a и ОУ, Ðγ- угол между a и OZ.
и ОХ, Ðβ- угол между a и ОУ, Ðγ- угол между a и OZ.
| i |
| β |
| y |
| O |
| х |
| j |
| γ |
| k |
| z |
| α |
Ðα= Ð (a,i), Ðβ=Ð (a,j), Ðγ =Ð (a,k).
cos α=  , cos β=
, cos β= 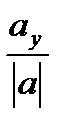 , cos γ=
, cos γ= 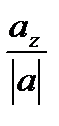 .
.
Свойство направляющих косинусов:
cos2 α+ cos2 β+ cos2 γ= 1.
Определение: Единичный вектор, имеющий своими координатами направляющие косинусы вектора a называется единичным вектором направления а и обозначается a0= (cosα, cosβ, cosγ).
| а |
| а0 |
Дата добавления: 2015-08-11; просмотров: 841;
